基于FPGA的超宽带数字下变频设计
1.引言
本文引用地址:https://www.eepw.com.cn/article/201710/367189.htm随着雷达应用需求的提高和数字信号处理技术的迅速发展,对雷达接收系统的设计也越来越希望符合软件无线电的设计思想,即将ADC尽可能靠近天线,将接收到的模拟信号尽早数字化。
数字化的中频信号通常基于FPGA实现数字下变频获得基带I/Q信号,但随着信号载频和带宽的不断提高,也需要更加高速的ADC完成信号采样,于是对数字下变频的处理要求也越来越高。在超宽带雷达接收系统中,高速的数据率使得基于FPGA的宽带数字下变频算法已不再适合采用传统的串行结构实现,本文介绍了一种基于并行多相滤波结构的超宽带数字下变频设计方法,其并行的流水处理方式使得高速数据无需缓存,处理带宽也相应大大提高。
2.设计原理
根据带通采样定理,在数字中频接收系统中采样率s f 与信号中频c f 。满足(其中M为正整数)时,数字混频算法最为简单,尤其是在采样率较高的超宽带数字接收系统中,满足此条件可以简化设计、便于工程实现。
在本文的超宽带数字接收系统中,采样率和接收带宽都较大,低通滤波器设计采用多相结构。设低通滤波器的冲激响应为h(n),其Z变换为:
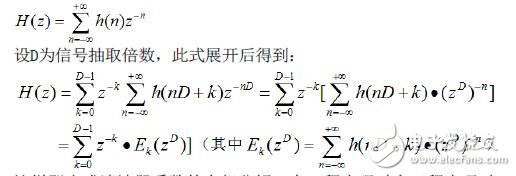
这样即完成滤波器系数的多相分解,在工程实现时在工程实现时,可以根据需要采用先抽取再滤波的方式降低对硬件处理速度的要求,并提高实时处理能力。
数字下变频仿真和设计主要基于FPGA系统级设计工具System Generator(SysGen)完成,它能够实现从算法模型向FPGA硬件的直接迁移。工程实现主要包含数字混频、并行多相滤波和数据抽取三部分,其中数字混频过程同时实现了2倍抽取,并行多相滤波后得到大带宽信号的基带I/Q数据,再对此基带信号进行2倍或多倍抽取即可实现对较小带宽的抽取。以并行八相滤波分解结构为例,数字下变频算法结构如图1所示。
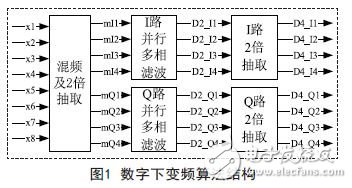
3.算法实现
本文的超宽带数字接收系统中,要求信号中频为400MHz,采样率为1600MHz,输入信号带宽包含600MHz和350MHz两种。根据后续处理系统需求,数字下变频后对基带信号分别进行2倍和4倍抽取,抽取后的数据率分别为800MHz和400MHz.
高速ADC选择TI公司的ADC083000,其采样率和全功率带宽均达到3GHz;FPGA选择Xilinx公司Virtex-6系列的XC6VSX315T,其具有较多的DSP48E资源,非常适合用于数字下变频算法中占用资源较多的数字滤波器设计。
3.1 高速数字信号预处理
ADC采样后的高速数字中频信号是通过4路速率为400MHz的并行总线输入至FPGA的,如此高速的信号显然不易在FPGA中直接进行数字下变频处理。为了适应FPGA进行数字下变频时的处理速度,保证其在常温和高低温下均稳定工作,首先需要对高速数字信号进行降速预处理。Virtex-6系列FPGA拥有专用的双倍数据速率寄存器IDDR可以实现数据率降低一倍,其下降沿数据由输入时钟的反转进行控制,算法实现如图2所示。
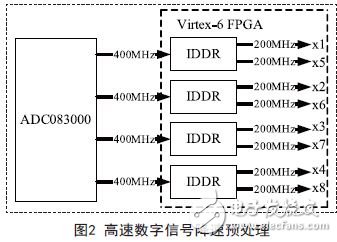
经降速处理后,输入至FPGA的4路并行、速率为400MHz的高速信号就变成8路并行、速率为200MHz的较低速信号,这样的数据率非常适合FPGA处理。
3.2 数字混频
由于信号中频400MHz与采样率1600MHz符合fc/fs=1/4的对应关系,数字本振就只有1、-1和0这样的简单序列,于是数字混频过程也就变成了加减运算。假设降速预处理后的8路并行信号为(x1,x2,x3,x4,x5,x6,x7,x8),则混频后I路并行信号为(x1,0,-x3,0,x5,0,-x7,0),Q路并行信号为(0,x2,0,-x4,0,x6,0,-x8,)。
本文中输入信号最大带宽为600MHz,因此数字下变频后抽取倍数最小应为2,而数字混频后I/Q各产生了4路并行为0的数据,这样混频过程中恰好可以实现2倍抽取,于是抽取后I路的4个并行支路信号为(x1,-x3,x5,-x7),Q路的4个并行支路信号为(x2,-x4,x6,-x8)。实际工程实现时,数字混频过程只需将输入的8路并行AD信号分成两组即可,加减运算与后面的并行多相滤波一起处理。
3.3 并行多相滤波
输入信号包含600MHz和350MHz两种带宽,为满足滤波器系数多相分解及重加载的需要,FIR低通滤波器统一设计为63阶、64个系数,频响特性如图3所示。
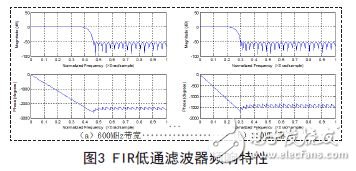
并行多相滤波算法最重要的环节就是系数分解,系数分解先进行二相分解,再各自进行四相分解,并获得8个支路I/Q信号的系数。
数字混频及2倍抽取后,I路信号仅保留了奇数支路,Q路信号则仅保留了偶数支路,并且滤波算法实际上是乘累加的线性卷积过程,这样I路低通滤波就仅使用FIR滤波器系数的偶数部分,同时Q路低通滤波就仅使用FIR滤波器系数的奇数部分,因此可以将滤波器系数首先进行二相分解。为满足系数重加载设计需求,并行多相分解后每个支路的系数长度应该一致,这样FIR低通滤波器系数的个数应为偶数N.假设滤波器系数为1 2 3 ( , , ,…, ) N h h h h ,二相分解后I路和Q路系数分别为2 4 ( , ,…, ) N h h h 和1 3 1 ( , ,…, ) N h h h 。
由于数字混频后I和Q分别含4个支路,为实现滤波算法的并行处理,需要对各自的滤波器系数进一步做四相分解,以得到各支路系数。这样实际上对系数完成了八相分解,因此滤波器系数的个数N应该为8的倍数。系数八相分解后,4个I支路的滤波器系数分别为2 8m h + 、4 8m h + 、6 8m h + 和8 8m h + ,4个Q支路的滤波器系数分别为1 8m h + 、3 8m h + 、5 8m h + 和7 8m h + ,其中m = 0,1,…, N / 8 ?1.
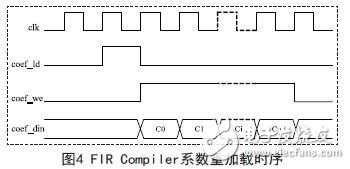
系数分解完成后,根据各支路多相滤波结构,在SysGen中采用FIR Compiler IP核实现算法设计。考虑到FPGA中除了实现超宽带数字下变频算法外,还包含接口与通讯、高速数据打包传输等功能,节省数字下变频算法在FPGA中的资源占用,两种信号带宽的滤波器采用系数重加载方式实现,其加载时序如图4所示。
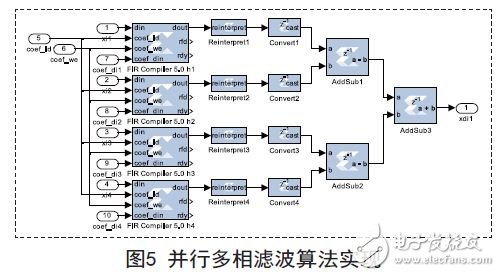
以I路的一个支路为例,SysGen中实现多相滤波的算法结构如图5所示,4路滤波输出求和过程同时实现了数字混频算法的加减运算。其余I支路以及Q路各支路滤波设计与此类似,仅延时有所不同,此处不再赘述。
经多相滤波处理后,I/Q分别得到并行4路、速率为200MHz的基带信号,将各自支路信号按顺序组合,即获得等效速率为800MHz的I/Q数据,也就实现了对600MHz带宽信号的数字下变频设计。
3.4 数据抽取
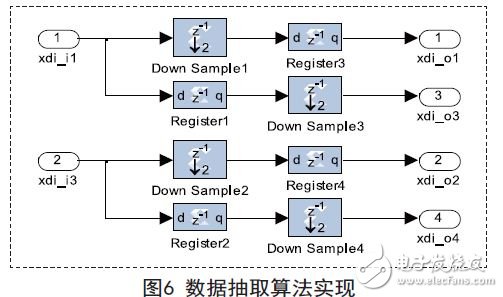
由于数字混频和多相滤波后的信号已完成了2倍抽取,要实现4倍抽取只需在此基础上再进行2倍抽取即可。考虑到后续数据处理的一致性,4倍抽取后的I/Q信号仍需要包含4个支路,选取各自多相滤波后的第1、3支路分别进行2倍抽取,SysGen算法实现如图6示。抽取后得到并行4路、速率为100MHz的基带I/Q信号,将各自支路信号按顺序组合即实现对350MHz带宽信号的数字下变频。
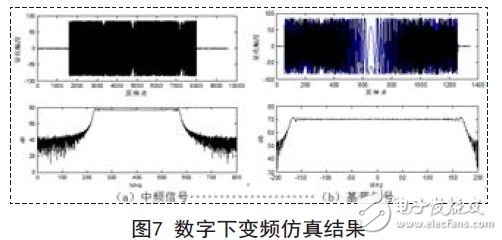
4.仿真应用
以350MHz带宽的线性调频信号为例,数字中频信号和数字下变频仿真结果如图7示。从图中看出,以并行多相滤波结构为基础的算法实现了数字中频信号的基带变换,且数字下变频后信号带内平坦度较好,满足工程应用需求。
限于本文中的采样率和并行处理结构,FPGA的运行时钟仅为200MHz,这对高性能的FPGA来说并不算困难。而对于更高速率的中频采样系统,只要FPGA的处理速度可以接受,那么仍然可以采用本文的算法结构实现。
5.结论
本文基于FPGA、以并行多相滤波结构为基础、在SysGen开发环境实现了超宽带中频信号的数字下变频算法,并通过仿真实验验证了可行性。设计参数中信号中频和采样率满足了带通采样定理约定的关系,这在一定程度上简化了数字混频设计;如果采样率和信号中频没有约定关系,那么可以在此设计基础上继续采用二次变频即可。















评论