基于FPGA的猝发式直扩载波同步技术研究与实现

　　在高动态环境中，由于载波多普勒频移和收发端时钟漂移等因素的存在，直扩接收机必须通过载波同步才能在接收端消除频差并重构载波相位，以实现相干解调。在传统的载波同步技术中，锁频环具有较大的捕获带宽但频率跟踪精度相对较低;锁相环虽然具有较高的跟踪精度却受到捕获带宽的限制。在同步时间要求不高的通信系统中，可以采用锁频环与锁相环级联的载波同步方法，使接收机既能承受环路带宽与动态性能之间的折中，又同时满足跟踪精度和一定动态性能。但本文所涉及的短时猝发式扩频通信系统要求更大的捕获带宽(±30kHz)，且导频符号仅为200个左右，同步时间要求极短。因此，双环切换载波同步方法在上述导频序列有限的直扩系统中很难快速实现大频偏捕获。为了兼顾动态性能、捕获时间和跟踪精度的要求，并结合猝发信号体制的特殊性，提出了一种在极低信噪比条件下，适用于长扩频码、大频偏情况的快速载波同步方案。

　　1 载波同步方案分析

　　载波同步包括载波捕获和载波跟踪。载波捕获采用扫频和FFT频率估计相结合的开环结构。扫频使频差减小到伪码捕获要求的频率范围内，以实现频率粗捕;FFT频率估计使频差进一步缩小，并进入Costas锁相环的快捕带内，以实现频率精捕;最后启动Costas环捕获并跟踪载波相位。载波同步流程图如图1所示。

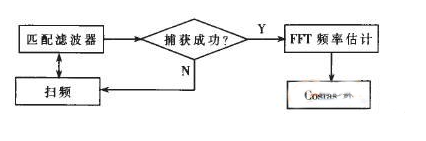
　　图1 载波同步流程图

　　1.1 频率粗捕

　　频率粗捕原理图如图2所示，匹配滤波器输出伪码相关峰值为：

　　式中，Ts为符号间隔，R(c(n))为伪码相关函数，△f为多普勒频偏，d(n)为有效数据。

　　图2 频率粗捕原理图

　　由式(1)可知，相关峰检测量对载波频偏和伪码自相关值具有敏感性。在高动态环境中，频率粗捕同时伴随着伪码捕获，实现频率粗捕需要在一个时域和频域构成的二维平面同时进行搜索。对多普勒频移的搜索可以将频率捕获范围分成多个区间串行或并行搜索完成;对码相位的搜索可以利用伪码的相关性通过相关运算完成码元搜索。

　　本方案中频率粗捕采用扫频和数字匹配滤波器相结合的实现结构。前者考虑到猝发系统导频符号有限，且同步时间要求极短，故采用如表1所示的快速扫频方式。在±30kHz的频率捕获范围内，扫频分两轮进行，分别以发射频率Ω和首轮锁定频点Ω为基准，以1.5Rs和0.5Rs为频率间隔，对表中参考频点进行串行搜索，取相关峰值最大时的频点作为捕获频点，从而将频差缩小到[-Rs/4，+Rs/4]以内，且以更少的导频符代价完成频率粗捕。后者以静止的本地伪码作为匹配滤波器系数，接收信号依次滑过本地伪码，每个时刻都产生一个相关值，当两个序列相位对齐时，相关值达到最大。若某时刻相关峰值大于捕获门限，则表明此时频率粗捕和伪码捕获成功，并记录码相位，开始解扩数据。匹配滤波器结构如图3所示。

　　表1 扫频频点设置

　　图3 数字匹配滤波器实现结构

　　1.2 频率精捕

　　由于频率粗捕和伪码捕获完成后，解扩信号中仍存在最大值为Rs/2的残余频差，而Costas环的快捕获带宽在1kHz以内。考虑到FFT运算可在一个符号时间内完成，所以可以利用FFT对载波频偏进行快速估计并将其缩小至Costas环的快捕带内。

　　本文采用N点固定几何结构的FFT运算方法，每级运算寻址结构相同，易于编程实现并行结构，从而加快FFT运算速度。FFT频率估计输入复信号如下：

　　其FFT变换为：

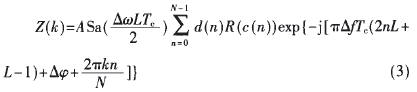
　　式中，N为FFT的采样点数。当Z(k*)为模值最大时，频偏的估计表达式为：

　　其中，Rs是符号速率。由于复信号的FFT变换是单边谱，当Af为正值时，kmax出现在(N/2～N-1);当△f为负值时，kmax出现在(0～N/2-1)。当△f被估计后，系统通过一次频率牵引，调整NCO频率控制字改变载波频率，使频差进一步缩小到[-Rs/2N，+Rs/2N]内。

　　1.3 载波跟踪

　　本方案采用Costas环实现载波的精确跟踪，原理结构图如图4所示。Costas环广泛应用于抑制载波调制信号的解调中，在捕获范围内有良好的跟踪性能，可以提供较低的误码率。

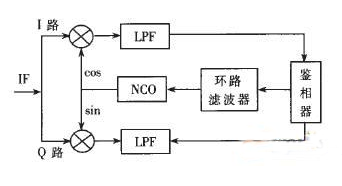
　　图4 Costas环原理结构图

　　Costas环鉴相函数为：

　　由于误差函数与频差和相差有关，当频差较小时，由频差引起的鉴相函数幅度衰减不大，此时Costas环可以正常工作。环路滤波器采用二阶结构如图5所示。传递函数为：

　　图5 环路滤波器结构图

　　环路滤波器的系数可以用来调整捕获带宽大小，可由以下公式来确定：

　　式中Ko为NCO增益，kd为鉴相器增益，ωn为环路自然角频率，ξ为阻尼系数。

　　2 载波同步方案实现

　　本项目采用DQPSK调制方式，系统时钟源为SF×m×Rs，SF为扩频因子，m为过采样率，Rs为符号率，码片速率为LxR1，L为Gold码长度，捕获范围为±30kHz，数据采用3帧间发方式，单帧长度为310个符号，由导频符和有效数据组成。

　　首先基于Matlab进行方案仿真，设定载波频率为20.46MHz，多普勒频偏为32.183kHz，输入信噪比为-19dB。试验中I路单帧数据长度为310个符号，经扫频消耗32个导频符号，I路剩余278个符号的解扩输出和对应原始发送数据如图6所示。由图6可见，解扩数据前32个导频符用于FFT频率估计，由于频差很大，解扩数据出错;在第32个导频符以后，即频差减小到1kHz以内，启动Costas环跟踪载波相位。对比图6(a)、(b)发现，有效数据在第146个符号后出现，数据正常解扩。有效解扩输出数据的星座图如图7所示，星座点在四象限中分布较为集中，表明信号可以正常判决恢复，采用本文提出的同步方案进行载波恢复效果明显。

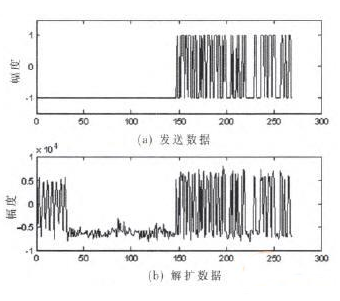
　　图6 发送与解扩数据比较

　　图7 解扩数据星座图

　　在利用Matlab完成方案的可行性验证之后，本文基于FPGA平台进行方案的编程下载，并通过EDA软件SignalTap工具实时捕获和显示信号，完成方案的硬件实现。试验中，接收信号频率为20.462825MHz，本地NCO输出频率为20.435MHz，载波频差为27.825kHz，符号速率Rs为10kHz。

　　频率粗捕的首轮扫频如图8所示。当伪码相关值较之前增大时，其值由quasipeak寄存。当没有信号进入时，quasipeak输出值较小，未能达到次轮扫频的阈值要求。因此频率控制字freq_mod_i修改本地NCO的频率，以15kHz的频率步进，不断来回扫描首轮5个频点。由图9可见，当有信号进入接收机时，quasipeak增大且达到次轮扫频阈值，则进入次轮细扫。次轮扫频完成后，freq_scan_complete置位，freq_mod_i保持5125不变，此时锁定捕获频点20.46MHz，相关峰值quasipeak较之前明显增大。当实时相关值达到伪码捕获阈值，即自相关最大值的0.75时，表明伪码捕获完成，同时捕获标志cap_peak_ok置位，并记录此时伪码相位，开始解扩数据。

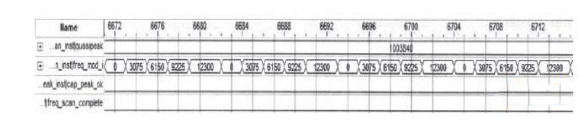
　　图8 首轮扫频

　　图9 次轮扫频与伪码捕获

　　FFT频率估计如图10所示。频率精捕采用32点FFT估计残余频偏，其最大值输出位置为24，由式(4)可知待校正频偏为2.5kHz(频率字为512)。经频率补偿后，phijnc_i为4194816，实际频率为20.4625MHz。由于伪码相关值较之前增大时，其值被quasipeak锁存。由图可见相关峰值较之前明显增大，表明通过FFT估计频率，使频差进一步减小到1kHz以内，频率精捕完成。

　　图10 FFT估计频率

　　Costas环相位跟踪的实际数据捕获图如11所示。在伪码捕获标志cap_peak_ok置位后，数据进行相关解扩，同时启动Costas环跟踪相位。)，为环路滤波器输出，vco为NCO相位控制字输入。由图11可见，载波频偏经过频率粗捕和精捕之后，进入Costas环的快捕带内，经过一个周期Costas环就跟踪上信号相位。dataLout为I路三帧间发数据的解扩输出，每帧导频符和有效数据在图中清晰可见，表明Costas环对信号相位进行了有效的跟踪。

　　图11 Costas环相位跟踪

　　单帧数据解调解扩输出如图12所示。接收数据经过载波同步后，需再进行差分译码和维特比译码才能得到有效帧数据。图12中，frame_data_out为单帧解扩数据，包括帧同步头、有效数据和CRC校验码，其与发送数据一致，表明有效数据经载波捕获和载波跟踪后，传输正确无误，系统工作正常。

　　图12 单帧数据解扩输出

　　本文结合猝发式直扩系统项目要求，利用步进扫频、FFT频率估计和数字Costas环实现了大频偏下载波频偏的精确同步，且捕获时间较短。通过Matlab方案仿真，Verilog编程下载和利用EDA软件SignalTap工具实时捕获和校验数据，验证了本文提出的载波同步算法方案的可行性，并具有较高的实际应用价值。