新型光学触摸屏的实现

　　CMOS摄像头放在触摸区域左上角，摄像头上绑有红外线LED灯。在触摸区域做一个垂直的固定装置用来放置两个反光条，反光条高度5毫米。LED灯照射在反光条上时，摄像头会抓拍到如图7所示的图像，图中出现亮暗相间的画面。

　　由于摄像头、红外线LED灯和两张反光条之间的角度，两反光条交汇的地方对应的图像区域亮点更密，即画面中对应于由A到B的区域亮点越来越密集，对应于由B到C的区域亮点变得越来越稀疏。由于图像亮点间隔的变化的规律性，在像素平面标示一个亮点只需要一维坐标，同时在触摸平面上标示反光条上的一点只需二维坐标。选B点所在位置为世界坐标系原点，BA所在的直线为坐标系x轴，BC所在的直线为坐标系y轴，在两个反光条上选取多个点，要求这些点在摄像头视野为亮点，(2-3)可简化为：

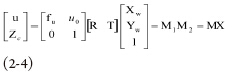
　　其中像素坐标系被设定为一维， u₀为光学中心，f_u为归一化焦距，世界坐标系设定为二维。R和T分别为摄像机坐标系到世界坐标系的2×2单位正交旋转矩阵和2×1平移矩阵，R含有一个未知参数，T含有两个未知参数，μ/Z_c为像素点在像素坐标系中的坐标，( X_w，Y_w )为触摸平面上一点在世界坐标系中的坐标。M₁为内参数矩阵，含有两个未知参数，只与摄像头自身相关，M₂为外参数矩阵，与摄像头所在的位置相关，含3个未知参数，M为透视变换矩阵。(2-4)相对于(2-3)把世界坐标系、图像所在的物理坐标系、像素坐标系都做了降维处理，把内参数矩阵、外参数矩阵做了降阶处理，这样就简化了内参数的求取过程。

　　2.3 方案所用摄像头各参数求解

　　2.3.1 内参数矩阵的求取

　　在触摸区域内移动附有反光条的垂直装置，每移动一次反光条的位置用左上角的摄像头拍下一幅亮暗相间的图像。拍下多幅图后，记录下每幅图中N个点(即图7所示的亮点对应于触摸平面上反光条上的点)在像素坐标系中的像素数。由于世界坐标系的坐标轴选取在BA、BC所在的直线上，反光条移动时这N个点在世界坐标系中的坐标不会发生变化。对于每幅图所选取的点的世界坐标和对应的像素数，根据式子(2-4)可求取一个内参数矩阵。对求取的多个内参数矩阵进行优化(Levenberg-Marquardt)优化以求取最优解。拍摄更多的图、每幅图选取更多的点进行计算，可有效地减少误差。本方案拍摄了5幅图，取N=17。

　　每幅图求取一个内参数矩阵的步骤如下：

　　1) 根据每幅图的17个点的坐标按照式(2-4)列出超定方程;

　　2) 用Levenberg-Marquardt算法优化透视变换矩阵;

　　3) 由透视矩阵分解出内参数矩阵和外参数矩阵;

　　4) 用Levenberg-Marquardt算法优化内参数矩阵;

　　设由五幅图求出的内参数矩阵、外参数矩阵、透视变换矩阵分别为：A_i、Rt_i 、ARt_i (i=1，2，3，4，5)，Rt_i对应的旋转矩阵和平移矩阵分别为R_i、T_i。由式(2-4)，设A_i的两个未知参数分别为a_i1、a_i2，R_i有一个参数，设为为r_i，T_i有两个参数，设为t_i1 、t_i2 。

　　用Levenberg-Marquardt算法优化内参数矩阵的步骤如下：

　　1)先优化Rt_i( i=1，2，3，4，5)的各项参数。假定A1较为精确，把A₁带入(2-4)求取第i幅图17个点的像素数误差之和ε_i(i=1，2，3，4，5)，εi 为关于r_i、t_i1、t_i2的函数，用Levenberg-Marquardt算法获取最优的r₁ 、t_i1、t_i2，使得ε_i最小。

　　2)优化完Rt_i再优化内参数矩阵A_i。对5幅图的r_i、t_i1、t_i2进行优化之后，求取5幅图的所有点的像素数误差加之和ε，此时ε为关于A₁中的参数a₁₁、a₁₂的函数，用Levenberg-Marquardt算法获取最优的a₁₁、a₁₂，使得ε最小。具体实验过程及数据如下：

　　5幅图中17个点的世界坐标是相同的，列举如表1 (单位mm)。5幅图中17个点对应的像素数列举如表2。

　　3)由透视矩阵分解出内参数矩阵和外参数矩阵，并把求取的内参数矩阵和外参数矩阵代入(2-4)求取每幅图对应的单点平均像素数误差，对实验数据保留两位小数，如表3所示。