基于汽车电子控制器的模态仿真技术研究
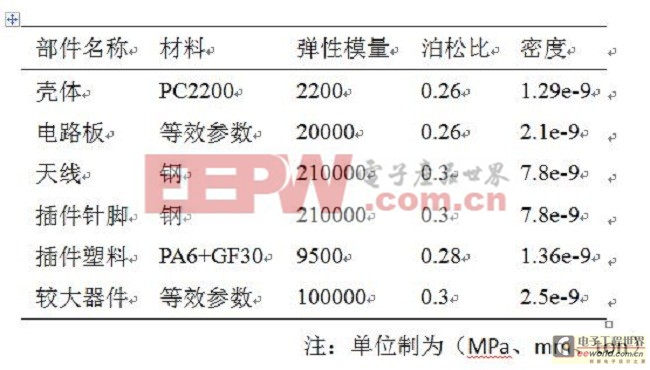
表1 各部件的材料参数
3.5仿真分析结果
利用Abaqus软件对该汽车电子控制器进行约束模态分析,得到的前三阶模态频率和模态振型如图9、图10、图11所示。第一阶固有频率为172Hz,第一阶振型为控制器沿两个安装耳中心点连线的前后振动;第二阶固有频率为262Hz,第二阶振型为控制器壳体上下面的相向的凸凹振动;第三阶固有频率为293Hz,第三阶振型为控制器壳体上下面的相对的凸凹振动。

图9 第一阶频率:172Hz

图10 第二阶频率:262Hz

图11 第三阶频率:293Hz
4 模态实验过程及结果
4.1模态试验过程
利用美国PCB公司的压电式力锤和压电式加速度计进行激励、拾振。然后用LMS TEST.LAB 试验采集分析系统进行数据采集和分析。试验设置为,采样频率为2048Hz,采样带宽为1024Hz,频率分辨率为0.125Hz,激励用力窗,响应是指数窗。
汽车电子控制器通过两个安装孔固定在基频大于500Hz试验台上。采用了5传感器布置方案(图12)进行模型试验。参照仿真分析结果发现,该传感器布置方案漏掉了第一阶扭转模态。而采用8传感器的布置方案(图13)能测得第一阶扭转模态。

图12 传感器的布置方案

图13 8传感器的布置方案
4.2典型的实验结果
在5传感器的试验中,若干点的频率响应函数如图14所示。随意选取一个测试点的相干函数如图15所示。在有效带宽的范围内,相干函数接近1,可以判定频率响应函数的可信度比较高。在8传感器的试验中,若干点的频率响应函数如图16所示。
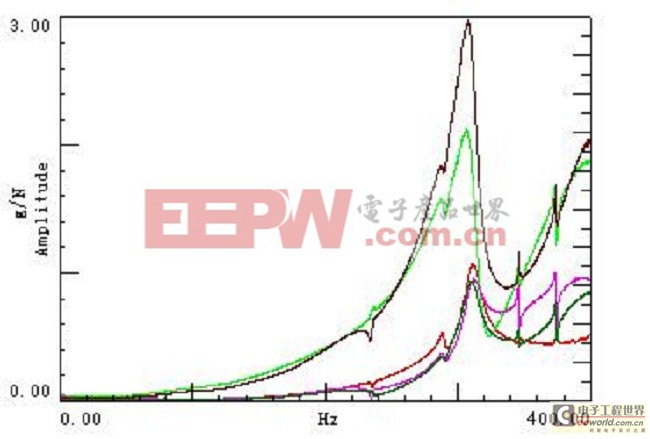
图14 若干点的频响函数
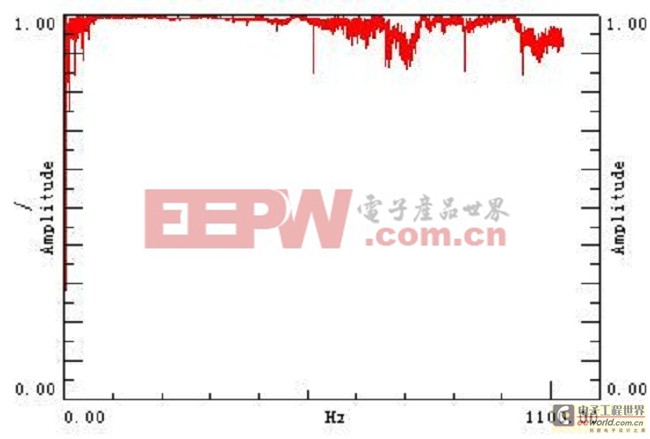
图15 典型相干函数
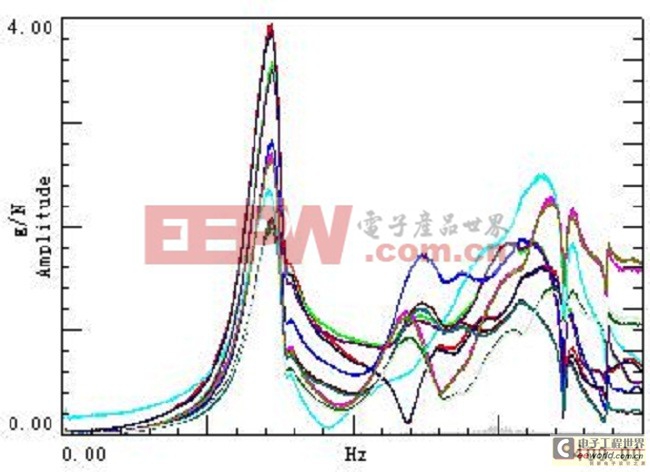
图16 若干点的频响函数
利用LMS TEST.LAB软件中的Time MDOF方法进行模态参数分析。根据所有测试点的频率响应函数之和建立稳态图,然后判定真实的模态频率、阻尼和参预因子。利用该方法测得的该控制器的前三阶模态频率和振型如图17-19所示。
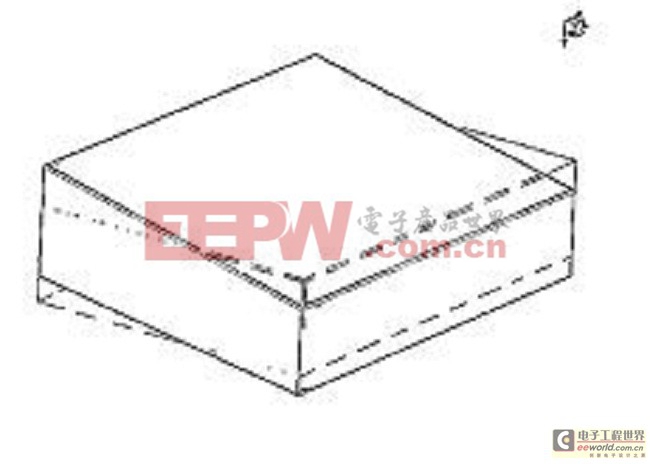
图17 第一阶模态: 146Hz
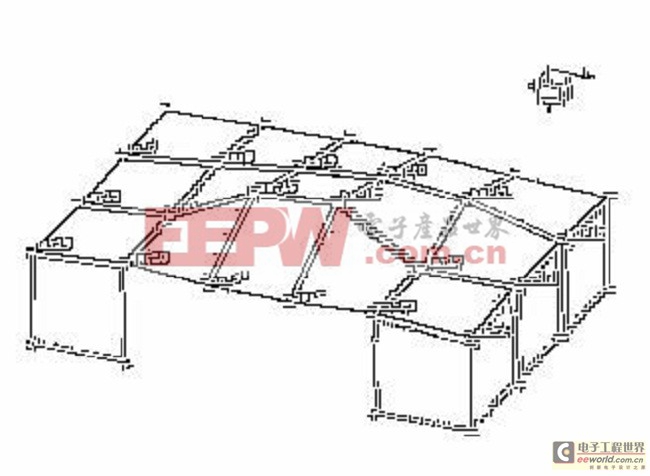
图18 第二阶模态: 236Hz
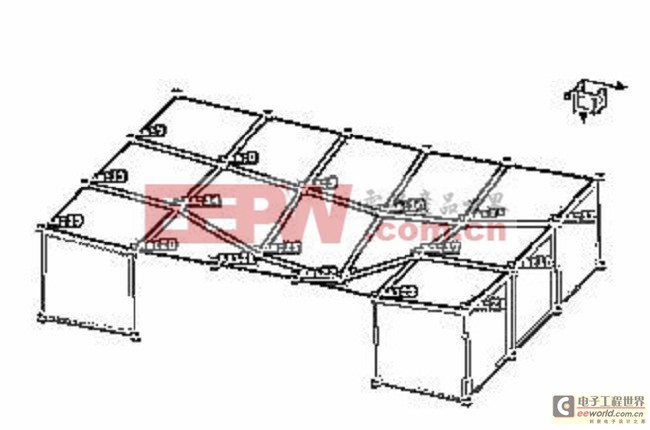
图19 第三阶模态:287Hz
5 计算和试验结果对比及分析
5.1仿真和试验结果对比
对比仿真分析和试验得到的前三阶振型,发现振型匹配很好;对比前三阶频率,发现最大相对误差将近20%,如表2所示。根据以上对比结果,可以判定该试验结果和仿真结果存在很大的误差。为了验证仿真分析方法是否可行,后文中将会对造成误差的原因进行分析。




评论