时钟域交叉与同步器（第一部分）：亚稳态建模

在超大规模集成电路（VLSI）设计中，时钟域交叉过程必然会出现亚稳态现象。要实现鲁棒且高可靠性的电路设计，必须对亚稳态进行抑制。想要掌握亚稳态的解决方法，以及如何设计满足指标要求的同步器，我们需要明确其产生原因、影响因素，以及降低其发生概率的方式。

亚稳态与触发器同步器

为了更深入理解时序元件进入亚稳态的过程，以及亚稳态的消解时长，可参考图 1。

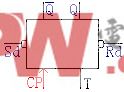
图 1：典型的主从锁存器触发器电路

图 1 为典型的主从锁存器触发器电路，由主锁存器和从锁存器组成，每个锁存器均包含两个级联的反相器。在正常且正确的工作状态下，时钟为低电平时，传输门 T₁ 导通，输入信号 D 传入主锁存器中由反相器 I₁ 和 I₂ 构成的闭环电路。

当时钟信号上升沿到来时，传输门 T₁ 关断、T₂ 导通，主锁存器中经过整形的输入信号随后传入从锁存器，经过一个触发器传播延迟（T_PCQ）后，信号最终在输出端 Q 稳定输出。

若假设时钟为低电平时，输入信号 D 和节点 A 的逻辑状态为 1，节点 B 的逻辑状态为 0；当输入信号 D 跳转为逻辑 0 时，节点 A 的电压开始下降，节点 B 的电压则随之上升。

若输入信号 D 的跳变发生在时钟有效沿附近，传输门 T₁ 会在节点 A 和节点 B 完成 0、1 逻辑状态的跳变前关断，此时两个节点可能进入亚稳态，被锁定在 1 和 0 之间的中间电压值，需要耗费不确定的时间，才能随机稳定至 0 或 1 其中一个逻辑状态。

亚稳态建模

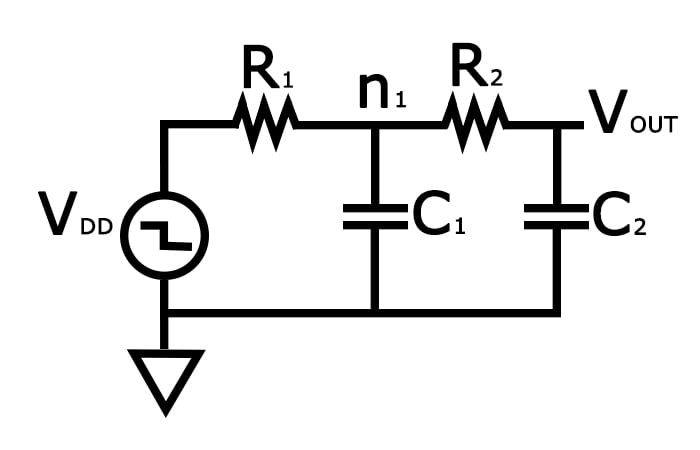
为了更清晰地理解亚稳态，以及锁存器稳定并脱离亚稳态所需的时间，我们将反相器建模为增益为 G 的负放大器，驱动传输门和另一个反相器的电阻 R 与容性负载 C（见图 2）。为简化分析，假设反相器的 PMOS 管和 NMOS 管驱动能力相同、阈值电压一致，中点电压 V_m = 电源电压 V_DD/2，随后求解节点 A 和节点 B 之间的电压差。

图 2：初始电压差随时间变化曲线

根据文献 ，该系统可通过如下公式建模：

其中，ΔV_in 为时钟有效沿切断输入 D 与节点 A 的连接时，节点 A 和节点 B 之间的电压差；ΔV_out 为经过时间 t 后，两个节点之间的电压差。

对于初始电压差为 ΔV_in 的情况，节点 A 和节点 B 的电压差达到电源电压 V_DD、亚稳态完成消解（即两个节点稳定至 0 或 1 逻辑状态）所需的时间 t_d，可由以下公式得出：

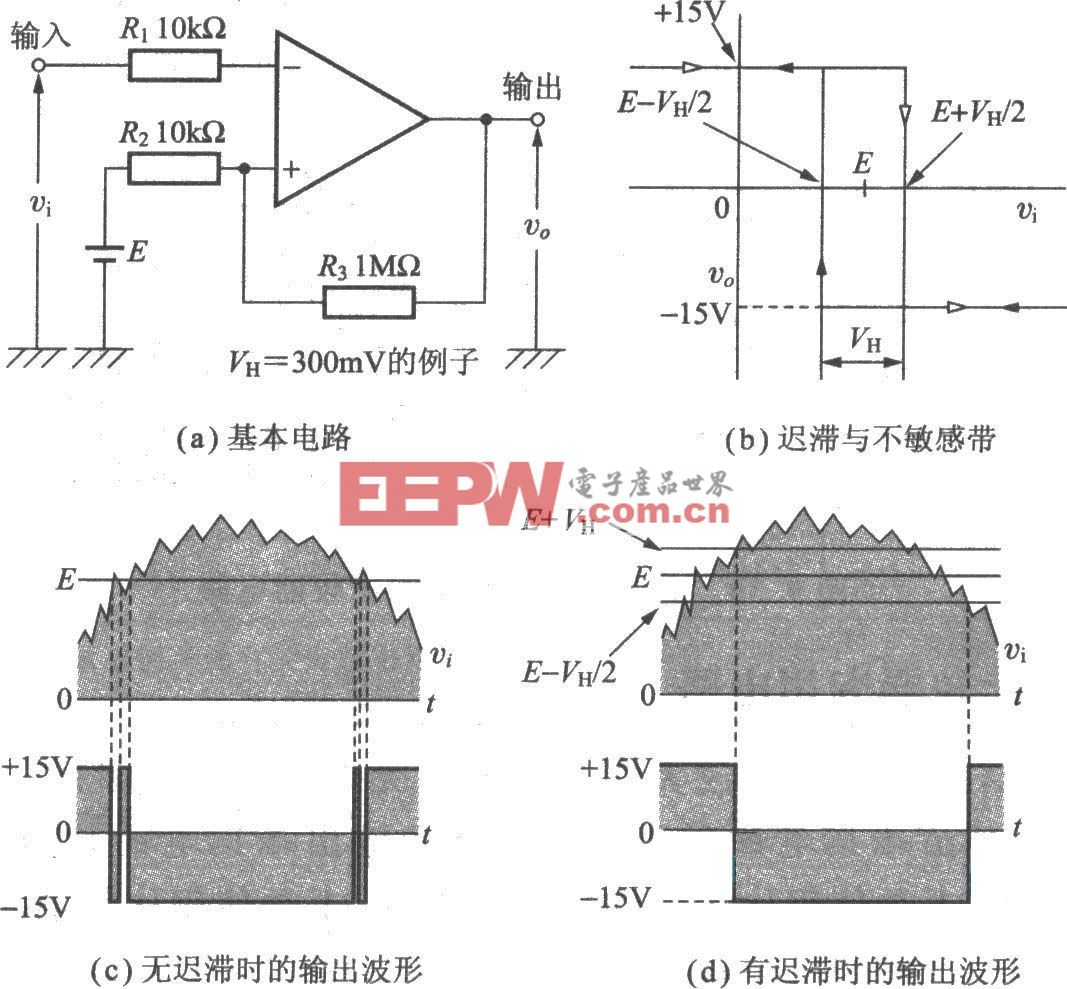
图 3 展示了初始电压差与亚稳态消解时间之间的关系。

图 3：输入电压差与亚稳态消解时间的关系曲线

当初始电压差 ΔV_in 较大时，节点 A 和节点 B 能快速稳定至对应的 1 和 0 逻辑状态；当初始电压差 ΔV_in 极小时，亚稳态的消解则需要耗费较长时间。公式 1 表明，输出电压差 ΔV_out 由初始电压差 ΔV_in 决定。

图 3 的上半部分曲线看似有违直觉，这是因为指数增长发生在极小的数值范围内；下半部分曲线则更具直观性，其以对数尺度描绘了节点间的电压差变化。

公式 2 同时表明，若初始输入电压差为 0（例如节点 A 和节点 B 的电压均为 0.5V），亚稳态的消解将耗费无限长的时间。但这一情况无需过度担忧，即便时钟上升沿切断输入信号时，两个节点的电压均为 0.5V，微小的热噪声也会打破这一平衡，最终使亚稳态得以消解。

综上，当数据在相位或频率不同的两个时钟域之间传输时，异步信号可能在采样时钟的跳变沿发生翻转，导致输出端进入亚稳态，在 0 和 1 之间的中间值震荡，直至经过公式 2 计算的 t_d 时间后，才会随机稳定至某一逻辑状态。至关重要的是，亚稳态必须在信号进入任何组合逻辑前稳定至有效逻辑值，以避免亚稳态在逻辑链路中传播。

进入亚稳态的概率

明确亚稳态无法避免，且知晓其消解所需时间后，我们接下来分析电路进入亚稳态的初始概率，以及在规定时间内无法消解亚稳态、进而导致逻辑失效的概率。

设时钟周期为 T_C，若数据输入在孔径时间 T_A 内发生变化，就会引发亚稳态现象。那么电路进入亚稳态的概率，即为可能进入亚稳态的时间与总时间的比值，计算公式如下：

其中，F_C 为设计的时钟频率。由于输入信号 D 并非每个时钟周期都会发生变化，定义每秒内的信号跳变速率为 F_D（即进入亚稳态的速率），则有：

电路进入亚稳态的平均间隔时间为：

以一个时钟频率为 2GHz 的设计为例，若触发器的建立时间为 15 皮秒、保持时间为 5 皮秒，其进入亚稳态的概率为 0.04；若输入信号的跳变速率为 400MHz（0.4×10⁹），则该锁存器每秒会进入 16×10⁶ 次亚稳态，即每 125 个时钟周期就会出现一次亚稳态，发生频率极高。

要计算亚稳态的失效概率，需先定义消解时间 T_r：主锁存器必须在该时间内完成节点 A 和 B 的状态稳定，避免亚稳态传播至从锁存器。主锁存器的消解时间 T_r,master 为半个时钟周期减去从锁存器的建立时间，而从锁存器的建立时间等于触发器的传播延迟 T_PCQ（即信号通过传输门 T₂ 和反相器 I₃ 的延迟），计算公式为：

主锁存器亚稳态消解失效的概率，等于电路进入亚稳态的概率，乘以在消解时间 T_r 内无法完成亚稳态消解的概率，即：

亚稳态消解失效的概率推导方式与亚稳态发生概率 P (MS) 一致。结合公式 1，假设完成亚稳态消解需要的最小初始电压差为 ΔV_in,min，且所有可能的 ΔVin 取值概率均等，那么在消解时间 T_r 内无法完成亚稳态消解的概率为：

由此可得整体失效概率为：

对应的平均失效间隔时间（MTBF）为：

触发器的失效概率计算，需同时考虑主锁存器进入亚稳态且消解失效的概率，以及从锁存器的相关概率，计算公式为：

其中，从锁存器的消解时间 T_r,slave为：

式中，t_setup 为第二个触发器的建立时间，t_pd 为从第一个触发器的从锁存器输出，到第二个触发器输入的级联延迟。触发器完成亚稳态消解所需的总时间 T_r,flop 可表示为：

若主从锁存器为相同规格的触发器，则 T_r,flop 的计算公式为：

由此可得单级触发器同步器的失效概率为：

假设时间常数 τ=35 皮秒，级联延迟 t_pd=0，那么 T_r,flop =500 - (2×15)=470 皮秒。上述同步器的失效概率为 58.9×10^-9，失效速率为 23.6 次 / 秒，对应的平均失效间隔时间由以下公式计算：

计算得平均失效间隔时间为 42.4 毫秒，该数值极低，意味着同步器极易失效。

综上，当数据在不同时钟域间传输时，进入亚稳态的概率可由公式 3 计算，触发器输出会在公式 2 计算的 td 时间内处于不稳定状态，直至亚稳态消解。

触发器同步器设计

若单级触发器同步器的亚稳态消解时间 t_d 超过一个时钟周期，无法在该时间内完成消解，或其平均失效间隔时间过短，可通过增加触发器级数的方式优化。增加级数能延长同步器在亚稳态传播至后续逻辑链路前的总消解时间  T_r,sync ，最终降低整体失效概率，提升平均失效间隔时间。

对于 n 级同步器，其失效概率为前序同步器级消解失效的概率，乘以最后一级同步器的失效概率，计算逻辑与公式 4 一致。若使用规格相同的触发器，且单级消解时间均为 T_r，则只需将指数项乘以同步器的级数即可。n 级同步器的失效概率和平均失效间隔时间计算公式为：

在上述示例中，若增加一级同步器，平均失效间隔时间将提升至 8 小时；若再增加一级，平均失效间隔时间可达 621 年。可见，由于亚稳态消解时间出现在指数项 e 中，同步器的平均失效间隔时间会呈指数级增长。

当计算得出的平均失效间隔时间达到 600 年左右时，看似系统已处于安全状态，亚稳态引发的系统失效会在很久后才发生，但实际情况并非如此。

设计中同步器的总数量，会直接影响系统的整体平均失效间隔时间。若单个同步器的平均失效间隔时间为 600 年，但设计中包含 600 个同步器，那么系统的实际平均失效间隔时间仅为 1 年，即每年都可能有一个同步器发生失效。

因此，在进行系统和同步器架构设计时，必须考虑同步器的使用数量，并计算其对系统整体平均失效间隔时间的影响，以避免突发失效。包含 K 个同步器的系统，其整体平均失效间隔时间计算公式为：

总结

由于时钟域交叉过程中的亚稳态现象无法避免，抑制其影响对保证设计可靠性至关重要。明确设计进入亚稳态的概率及其失效概率，是选择或设计高平均失效间隔时间同步器的核心，唯有如此，才能确保电路设计的可靠性和鲁棒性。