基于LabVIEW仿真的全局最短路径的遗传算法设计
加入技术交流群
判断矩阵A1、3、4、5的行向量线性不相关，秩是列数4，也就是被选中的线段个数即每个个体的基因数。个体{1、2、5、10}因为1、2、5构成了回路，可以得到
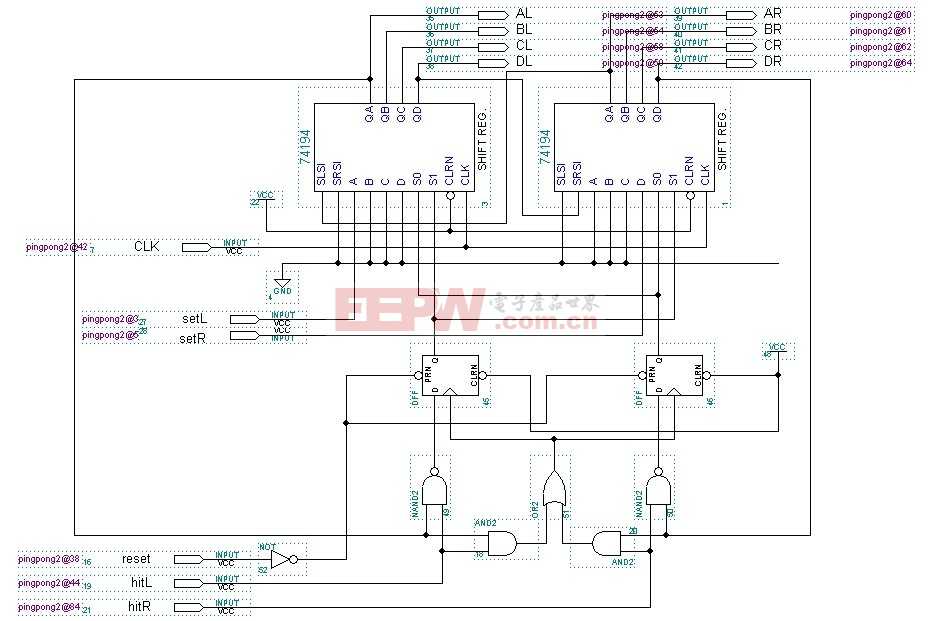
，其判断矩阵A1、2、5、10中对应的3个行向量必定是同样的关系，则这3个行向量线性相关。所以判断矩阵A1、2、5、10的秩必然小于列数4。由矢量图能看出，每多一条回路，判断矩阵的秩就会减少1。当出现重复编号时，如{1、1、2、5}，则有2个行向量相同，其判断矩阵A的秩必然也小于列数4。综上，Point[]是已知的。由Point[]可以得到Line[](如图3(a))。任意给定4条线的个体，由Line[]和Point[]得到判断矩阵A，如果rank(A)=M-1，则满足3个条件(如图3(b))；否则，该个体非法。本文引用地址：https://www.eepw.com.cn/article/202494.htm
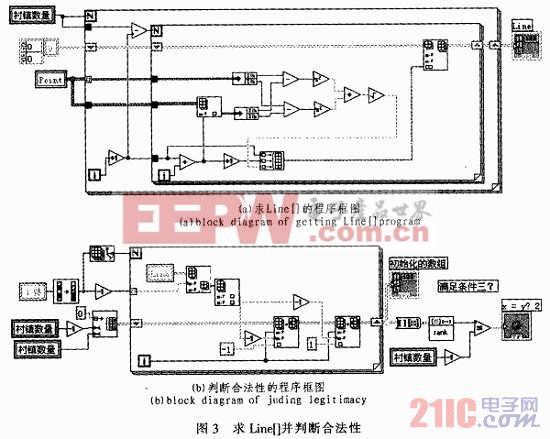
3 初始种群获取
根据上面的说明，本文在获取初始种群时，每一个个体首先是从M(M-1)／2条线段中随机取出M-1条。取得的方法是：
1)建立M(M-1)／2阶布尔数组，数组里每个元素是假常量；
2)产生一个0～1的随机数与M(M-1)／2相乘并向下取整，随机得到一个整数n，则n∈[0，M(M-1)／2-1]；
3)将布尔数组中第n个元素替换为真常量；
4)重复2、3步直到布尔数组中有了M-1个真常量；
5)依次提取布尔数组中的每个真常量的索引值并加1。
其取得方法的框图如图4所示。
得到的M-1阶常数数组就是一个随机产生的初始个体，而且此个体直接满足条件1和条件2。对这样的个体进行合法性判断，如果不合法舍去重新产生新个体。如果合法保留再生成下一个个体。用for循环来控制种群大小。
4 适应度函数
因为目标函数是求最小值，而且D肯定大于0，所以不妨直接以目标函数的倒数作为适应度函数。
5 遗传策略
本文基于Srinivas提出的自适应遗传算法(Adaptive GA，简称AGA)提出新的编码方式下的遗传策略。
式中，pc表示交叉率，Pm表示变异率，fmax表示种群最大适应度值favg表示种群平均适应度值，f表示在要交叉的两个个体中较大的适应度值，f表示要变异的个体适应度值。k1，k2，k3，k4是在0和1之间取值的常数，其中，k3和k4较大。
式(3)和式(4)是AGA根据适应度值调节后的交叉率和变异率，它较好地解决遗传算法中全局搜索和局部搜索的平衡问题，提高了收敛速度。
5．1 杂交
杂交运算是遗传算法扩大优秀基因影响的重要方法。但本文使用的编码方法中，如果使用简单的单点交叉方法，无疑很大概率上将产生不合法的无效子代。如图1中的5个点，两个父代{1、2、3、4}和{4、5、8、10}做交叉运算，无论交叉点在哪都会产生含有2个4号线段的非法子代。不满足条件1。
评论