基于状态变量摩擦模型的振动控制*
*基金项目:2020年产业技术基础公共服务平台——工业机器人核心关键技术验证与支撑保障服务平台建设项目(2020-0097-1-1)
本文引用地址:https://www.eepw.com.cn/article/202108/427334.htm作者简介:梁学修(1987—),男,山东青岛人,博士,研究方向为智能检测与控制。
0 引言
非线性摩擦是影响工业机器人低速运动性能的主要因素之一,机器人关节摩擦力会使机器人产生跟踪误差,带来极限环振荡、滞滑运动等问题[1]。为此,对机械臂的非线性摩擦建模与补偿研究成为工业机器人控制领域的研究热点[2-6]。为了解决关节摩擦力的问题,通过实验总结出了各种摩擦力模型。建立机器人关节摩擦模型是实现摩擦力实时补偿的核心步骤。摩擦的时变、强非线性等性质,使得精确建立摩擦力的模型几乎无法实现。工程中使用的静态摩擦模型和动态摩擦模型[7]也仅仅是摩擦力模型的一种近似模型。借助这种近似的摩擦力模型,只能在一定程度上消弱摩擦力的影响。在静态摩擦模型中,应用最广泛的是图1 中的Stribeck 指数模型[8],该模型对真实摩擦力的拟合精度达80%。本文研究了在极低速度下如何实现稳定控制的问题,通过摩擦建模,引入了考虑瞬态摩擦的状态摩擦模型,通过基于状态变量摩擦模型的动力学方程,完成了基于状态摩擦模型的动力学方程的稳定性分析。
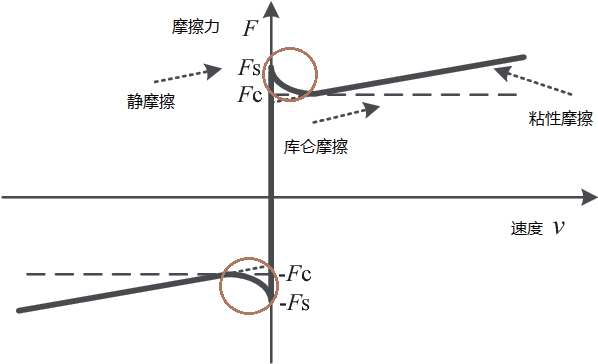
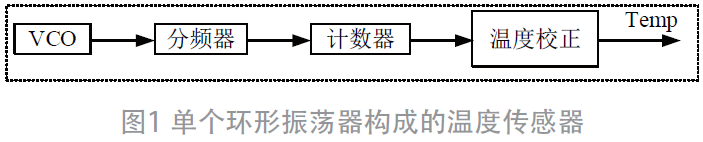
图1 Stribeck模型
1 摩擦力模型
刚体材料之间通过润滑剂润滑时的特征摩擦- 速度曲线就是图1 中所示Stribeck 曲线。通常由静摩擦fs 、库伦摩擦fc 和黏性摩擦构成。在相对运动的方向没有逆转的条件下,接触面稳定滑动的摩擦力是速度的连续函数。这条曲线的斜率取决于材料的成分和它们之间的润滑状况。对于圆圈标记出的低速范围,曲线存在一个陡峭的负斜率段,这一段正是本文将要讨论的低速区摩擦- 速度曲线。
通常用于模型补偿的摩擦- 速度曲线,包括Stribeck曲线,代表稳定滑动的摩擦。摩擦力模型只依赖于当前的速度值。然而,摩擦实验[9]表明,摩擦也取决于过去的运动历史。
Sampson[10] 等人最早注意到摩擦力的这种现象。考虑过去的运动历史,摩擦力模型f(t) 的函数关系可以表示为:
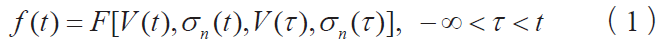
其中, V 为接触面相对滑动速度, σ n 为法向压应力。也就是说摩擦力不仅仅和当前时刻的速度V t ( ) 和法向压应力σ n(t)有关,还和过去时刻的速度V (τ )和法向压应力σ τ n( )有关。
本文考虑的状态变量摩擦模型具有以下3 个特征(假设正应力恒定):
● 依赖于速度的摩擦力稳定状态;
● 依赖于速度的摩擦力瞬时状态;
● 特征滑移距离。
依赖于速度的摩擦力稳定状态就是摩擦力- 速度曲线。依赖于速度的摩擦力瞬时状态就是速度的瞬时变化导致摩擦力在同一方向上的瞬时变化。第3 个性质表示的是当速度突然变化时,摩擦力指数衰减到稳态的摩擦力- 速度曲线需要滑动的距离。对于法向应力为常数的情况,状态变量摩擦模型具有下面的摩擦力模型:
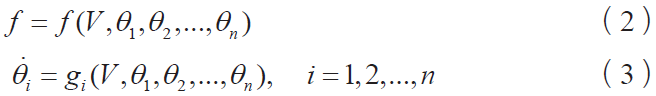
等式中θi表示状态变量,这种形式表明,速度的突然变化不会引起状态的突然变化,但会影响它的时间导数。稳定状态的摩擦力- 速度曲线可以通过设置gi为零,而后将状态变量θi替换到函数f 中得到一个非常简单的包含单个状态变量的摩擦模型:
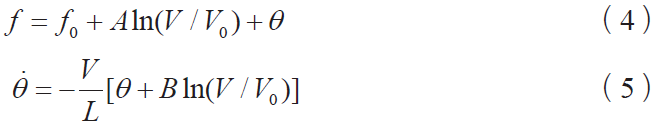
L特征滑移距离( f0 ,V0) 对应于稳态摩擦- 速度曲线上任何合适的初始点。在这种情况下,稳态摩擦- 速度曲线为:
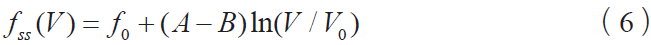
稳态摩擦- 速度曲线中常用速度指数项表示从静摩擦到动摩擦的过渡。一种包括库仑摩擦和黏性摩擦的模型为:
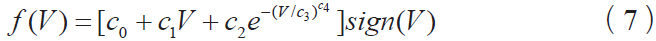
其中c0,c1,c2,c4>0。状态变量摩擦模型是专门为模拟摩擦的低速效应而设计的,而稳态摩擦模型是用来制定适应整个运行速度范围的模型。
2 考虑摩擦的动力学模型
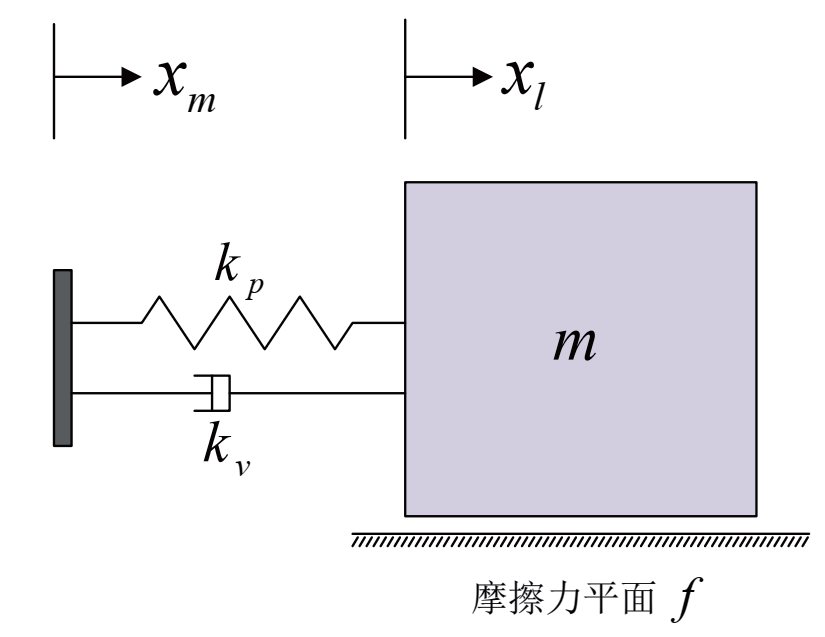
图2 关节模型
图2 给出了一个具有代表性的机器人关节的动力学模型, xm 和xl 分别代表电机和关节的位置, kp 代表关节刚度或是控制增益,kv 代表附加阻尼,m是连杆质量,f 则代表关节摩擦模型。位置控制的动力学方程:
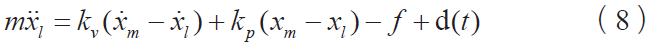
不考虑扰动d(t)的情况下,由于关节摩擦f的原因,机器人在稳定运行状态下会产生恒定的偏置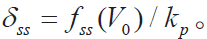 在考虑扰动d(t)的情况下,连杆的速度存在微小的偏置
在考虑扰动d(t)的情况下,连杆的速度存在微小的偏置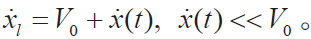 最终的扰动动力学方程为:
最终的扰动动力学方程为:
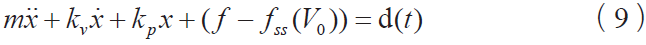
3 稳定性分析
假设法相正应力恒定,考虑依赖于当前速度和滑动历史的摩擦定律:
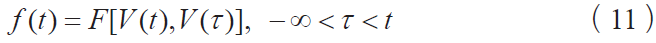
假设摩擦力f t ( ) 可以被分离为1 个瞬态分量和1 个稳态分量。后者趋向于在特定速度下滑移足够距离时的稳态值。在本文讨论的低速区,稳态摩擦- 速度曲线的斜率是负值,也即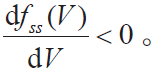
依据Rice and Ruina[11],用脉冲响应表示f(t) 在平衡点附近的线性化行为,摩擦力模型可以表示为:
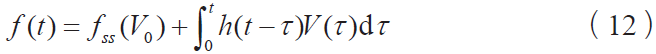
认识到速度的直接影响是一个脉冲函数,可以把它从卷积积分中提取出来,
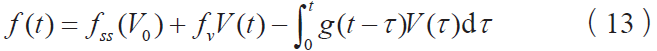
结合这个方程,摩擦力关于速度的瞬态变化率为:

摩擦力关于速度的稳态变化率为:

实验表明[11],摩擦与速度的瞬态关系为正,也即fv > 0 。对于负斜率的稳态摩擦曲线,

为保证摩擦力是单调递减的,g(t) 需要满足条件:

将式(13)代入式(9),得到关节的动力学方程为:
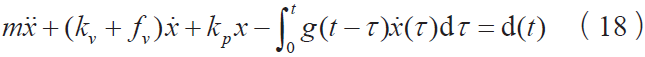
做拉普拉斯变换,得到:
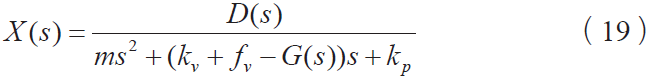
3.1 考虑当前速度摩擦力模型的稳定性分析
考虑简单情况的摩擦律f=f(V(t)),即不考虑过去的运动对摩擦模型的影响,也即:

稳定性是由X (s)的极点位置决定的,在这种简单的情况下考虑下面等式的取值:

由于m > 0,如果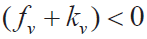 就会发生不稳定性。如果摩擦系数fv 在V0 处斜率为负,需要附加阻尼kv 实现稳定, 可以选择
就会发生不稳定性。如果摩擦系数fv 在V0 处斜率为负,需要附加阻尼kv 实现稳定, 可以选择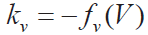 的最小值, 对于0 <V <Vmax ,以实现整个速度范围内的渐进稳定。在这个线性分析中,对kp 的唯一要求是kp > 0 。
的最小值, 对于0 <V <Vmax ,以实现整个速度范围内的渐进稳定。在这个线性分析中,对kp 的唯一要求是kp > 0 。
例如,考虑下面的摩擦力形式:
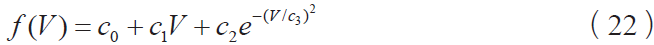
在这种情况下:
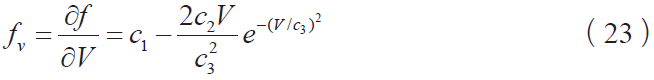
如果fv < 0 ,则需要一个正的kv 来稳定系统。令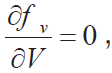 可得
可得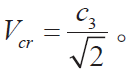 为了满足渐进稳定的条件,附加阻尼系数需要满足
为了满足渐进稳定的条件,附加阻尼系数需要满足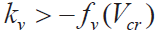 ,其中:
,其中:

3.2 状态变量摩擦力模型的稳定性分析
分析使式(19)稳定需要的控制增益。考虑下面等式的根:
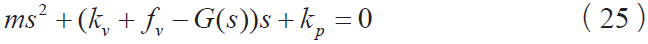
下面考虑kp 的所有可能取值:
①当kp →∞。由于G(∞) = 0,解的实部为:

由于fv 和kv都是正的,故而Re(s) < 0恒成立。因此,kp → ∞ 条件下,等式(25)始终能够保持稳定;
②当kp = 0,考虑方程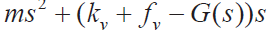 。考虑到式(27),此方程对于小的s 是负的,对于大的s 是正的,故此时系统无法保持稳定。
。考虑到式(27),此方程对于小的s 是负的,对于大的s 是正的,故此时系统无法保持稳定。
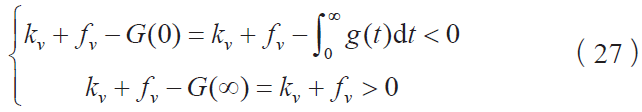
③考虑上述内容,当kp 从零到无穷,存在一个根或1 对根穿过虚轴。将s = 0 和s = ∞ 代入等式(25),因为m 、fv 、kv 和kp 都是正的,可知方程无解。因此解如果存在,其只能是一对虚根±iω ,且和kp 的临界值kcr 有关:
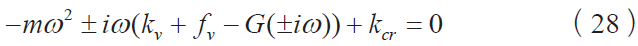
将上述方程分解为实部和虚部,得到ω 和kcr 的方程:
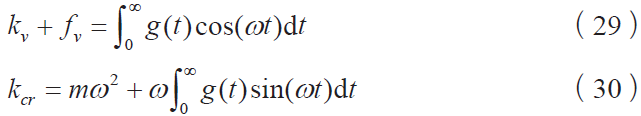
使用我们的假设g(t)≥0,并得到
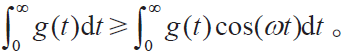 我们发现式(30)只有在满足下面条件的时候才有解:
我们发现式(30)只有在满足下面条件的时候才有解:
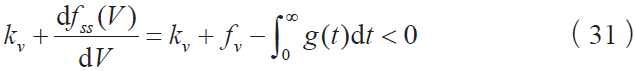
稳定性结果总结如下:
对于考虑摩擦律f = f [V (t)]的动力学模型,渐近稳定的条件为:
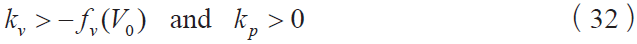
对于考虑摩擦律 f = f [V (τ )], 0 <τ < t 的动力学模型,渐近稳定的条件为:
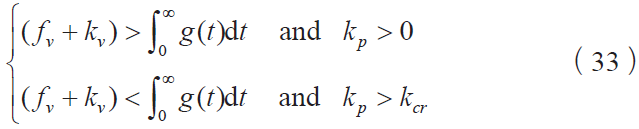
这样可以依据式(32),根据仅考虑当前速度的摩擦力模型,选择合适附加阻尼kv 来保证动力学系统的稳定性。可以依据式(33),根据同时考虑过去运动状态和当前速度的状态变量摩擦模型,选择合适的k k v p 、来保证系统的稳定性,而k k v p 、就是系统的控制参数。
4 结束语
实现稳定的低速度运动能力对机器人和任何涉及精细定位或力控制任务的机器来说都非常重要。然而,在实际应用中,高度非线性的摩擦力会产生一个最小的稳定速度,低于此速度就会发生粘滑,严重限制机器人位置和力控制的精度。此外,滞滑摩擦力引起极限环是机械振动的一个主要诱因。
本文研究了用状态变量摩擦模型表示低速运动中的瞬态摩擦,并提出了基于状态变量摩擦模型的动力学方程的稳定性证明,依据稳定证明给出了控制参数设置的合理指导。
参考文献:
[1] KERMANI M R, WONG M, PATEL R V, et al. Friction c omp e n s a t i o n i n l o w a n d h i g h - r e v e r s a l - v e l o c i t y ma n ipula to rs[C]// Robo tics a n d Automa tio n , 20 0 4 .Pr o c e e d i n g s . I C R A ‘ 0 4 . 2 0 0 4 I EEE I n t e r n a t i o n a l Conference on. IEEE, 2004.
[2] TOMEI, P. Robust adaptive friction compensation for tracking control of robot manipulators[J]. IEEE Transactions on Automatic Control, 2002, 45(11):2164-2169.
[3] IWATANI M, KIKUUWE R. An identification procedure for rate-dependency of friction in robotic joints with limited motion ranges[J]. Mechatronics, 2016, 36:36-44.
[4] QIN J, LÉONARD F, ABBA G. Real-Time Trajectory Compensation in Robotic Friction Stir Welding Using State Estimators[J]. IEEE Transactions on Control Systems Technology, 2016, 24(6):2207-2214.
[5] ROVEDA L, PALLUCCA G , PEDROCCHI N , et al.Iterative Learning Procedure with Reinforcement for High-Accuracy Force Tracking in Robotized Tasks[J]. IEEE Transactions on Industrial Informatics, 2017:1-1.
[6] SIMONI L, VILLAGROSSI E , BESCHI M , et al. On the use of a temperature based friction model for a virtual force sensor in industrial robot manipulators[C]// 22nd IEEE International Conference on Emerging Technologies And Factory Automation (ETFA2017). IEEE, 2017.
[7] BONA B, INDRI M. Friction Compensation in Robotics: an Overview[C]// European Control Conference Cdc-ecc 05 IEEE Conference on Decision & Control. IEEE, 2005.
[8] BO L C, PAVELESCU D. The friction-speed relation and its influence on the critical velocity of stick-slip motion[J]. Wear,1982,82(3):277-289.
[9] RUINA A. Friction laws and instabilities: A quasistatic analysis of some dry frictional behavior[D]. Providence:Brown University,1980. Sampson J B,MORGAN F,REED D W.Friction Behavior Duringthe Slip Portion of the Stick-Slip Process.Journal of Applied Physics,1943,14(12):689-700.RICE J R, RUINA A L. Stability of Steady Frictional Slipping[J]. Journal of Applied Mechanics, 1983, 50(2):343-349.
(本文来源于《电子产品世界》杂志2021年5月期)





评论