模拟采样质量：精确度、灵敏度、精密度和噪声

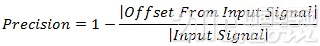
等式4:计算精密度

比如，如果您正在监测1V的恒定电压，您会发现如果测量值之间相差20 µV,则可以通过以下公式计算出精密度：

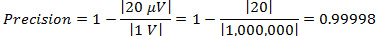
通常情况下，精密度用百分比表示。 在这个例子中，精密度是99.998%。

当需要进行相对测量时(同一测量值与前一个读数的差值)，比如对设备进行校准时，精密度具有重要意义。

4. 噪声和噪声源

噪声是指所有对有用信号产生影响的干扰信号。 噪声会在测量过程中引入不确定性，这种不确定通常会随时间而变化。 这种不确定性可以是随机的也可以是周期性的。 噪声可以是瞬态噪声也可以是宽频随机噪声，其中瞬态噪声具有固定频率，比如谐波或混频产物。 有时候我们会认为噪声不会影响精确度规范，因为我们可以使用平均值或其他技术来消除噪声。 然而，在大多数情况下精确度规范中包含了噪声。 规范文件中应该规定噪声是否包含在其中，通常情况下这些信息在脚注中给出。

噪声有许多来源。 被测源或被测项可能会产生固有噪声。 有些噪声可能来自热辐射源，比如电阻器噪声，也可能是内在噪声，比如由半导体设备产生的噪声。 同样，噪声可能源自于外部环境，比如输电线、房间中的灯光、电机和射频源(比如无线电发射机、手机、无线电台等等)。

热噪声

理想的电子电路不会产生噪声，因此这种电路产生的输出信号仅包含原始信号的噪声。 但是实际电子电路和组件会产生一些固有噪声。 即便是简单的固定值电阻器也会产生噪声。

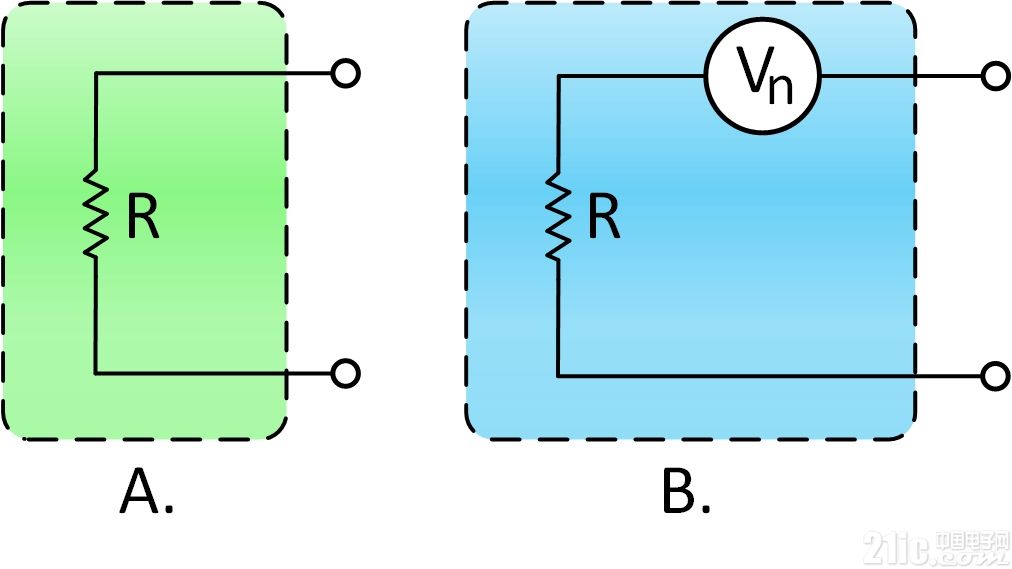
图4.图A显示的是一个理想的电阻器，但实际电阻器具有内部热噪声，如图B所示。

图4A给出了一个理想的、无噪声电阻器的等效电路。 固有噪声如图4B中所示，该图将噪声电压电源Vn与理想、无噪声的电阻Ri串联。 在高于绝对零度(0°K或大约-273°C)的任何温度下，任何材料中的电子都在作恒定的随机运动。 然而由于电子运动本身具有随机性，因此在任何一个方向上都无法探测到电流。 换言之，任何方向的电子漂移都在很短的时间内被反方向的等量漂移所抵消。 因此从统计学角度来看，电子运动不具有相关性。 然而，材料会产生一系列连续的无规则电流脉冲，这些脉冲在外界看来就是噪声信号。 这种信号有多种名称： 约翰逊噪声、热骚动噪声或热噪声。 这些噪声随着温度和电阻的增大而增大，而且是以平方根函数的方式增大。 这意味着如果要使噪声变为原来的两倍时，电阻需要增加到原来的四倍。

闪烁或1/F噪声

半导体设备的噪声通常不平行于频率。 它在下限处产生， 此时的噪声称为1/F噪声、粉色噪声、过量噪声或闪烁噪声。 这种类型的噪声除了在电子系统中产生外也在物理系统中产生。 比如，蛋白质、认知过程的反应时间甚至是地震活动。 下图给出了噪声最有可能的来源，这些来源取决于噪声在特定电压下产生的频率;知道噪声来源对于减小噪声具有重要作用。

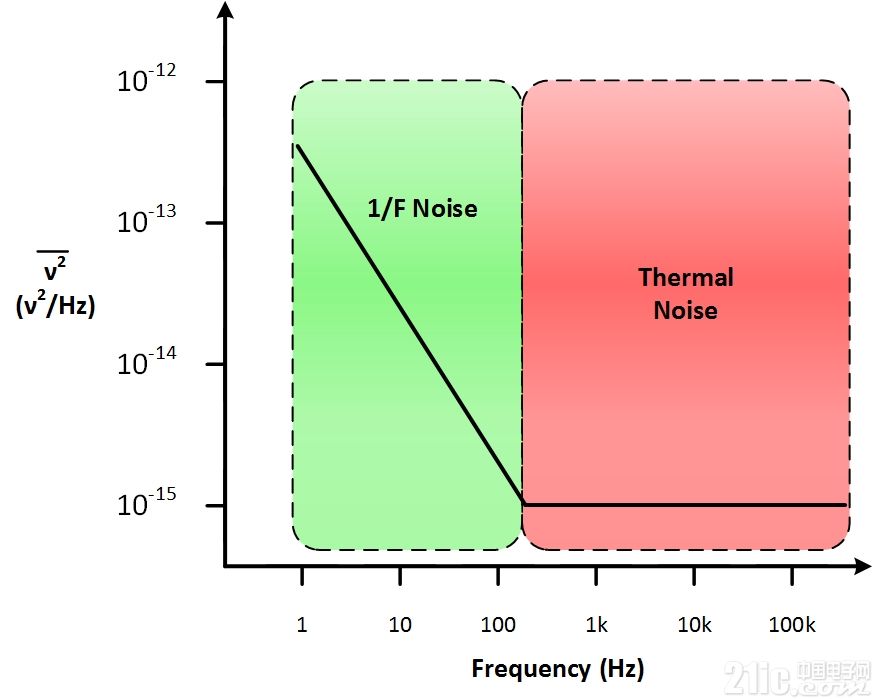
图5.1/F噪声和热噪声的噪声谱剖面图

5. 降噪方法

虽然噪声对于设计工程师来说是一个严重的问题，特别是对于低电平信号情况，但是也有许多常用的方法可以减小噪声对系统的影响。 以下一些可以降噪的方法：

源电阻和放大器输入电阻使用尽可能低的阻值。 使用高阻值电阻可按比例提高热噪声。

热噪声的值是电路带宽的函数。 因此，可以通过减小电路的带宽来使噪声最小化。 但是这项工作须小心进行，因为信号具有傅里叶谱，我们需要保留傅里叶谱才能对信号进行精准测量。 解决方法是将带宽与输入信号所需要的频率进行匹配。

我们可以通过合理接地、屏蔽、布线、谨慎地放置电线和滤波来改善系统的性能，进而防止外部噪声。

在系统的输入阶段使用低噪放大器。

对于一些半导体电路，可以使用最小直流电源来实现该目的。

6. 总结

灵敏度是指可以让测量仪器做出响应的输入信号的最小变化量。

精确度是指仪器可以如实地显示被测信号值的能力。

精确度和灵敏度会在规格文件中写明;由于不同公司或者同一公司的不同产品对这些术语的定义各不相同，因此要经常查看文档，如有疑问应与供应商联系确认。

精密度用来描述仪器测量的稳定性以及在输入信号相同的情况下多次测量结果保持一致的能力。

噪声是指所有对有用信号产生影响的干扰信号。

不同类型的噪声有不同的降噪方法。