基于DSP的双极性双调制波高频链逆变器实现

定时器GP工作在连续增减计数模式，即从零开始递增计数至设定值，然后又递减计数至零，如此循环，计数周期为开关管的一个开关周期。

高频逆变桥各开关管的驱动信号为ugVS1，VS4，ugVS2，VS3，其产生过程较为简单。如图3所示，当定时器工作在增计数模式时，UgVS 1，VS4为高电平，ugVS2，VS3为低电平，而当定时器工作在减计数模式时，ugVS1，VS4为低电平，ugVS2，VS3为高电平。无论输出电压为何值，均在定时器计数至周期值或零时发生跳变，即计数值与比较寄存器值在H，H’点匹配。

周波变换器的控制信号为ugVS5，ugVS6，ugVS7，ugVS8，在图3a中，当定时器工作在增计数状态时，计数值与比较寄存器值在I点及J点发生比较匹配，ugVS5，ugVS8为高电平；当定时器工作在减计数状态时，计数值与比较寄存器值在I’点及J’点发生比较匹配，ugVS5，ugVS8跳变为低电平。ugVS6，ugVS7分别与ugVS5，ugVS8互补，则可以产生4路移相PWM控制信号，移相角随正弦规律略有变化。

图3b与图3a原理类似，只是ugVS5，ugVS7从超前臂变为滞后臂，VS8，VS6从滞后臂变为超前臂。载波比较示意图如图3c所示，其中ur为调制波，um为其反值，uc为双极性的三角载波，Tc为载波周期，A为正弦调制波幅值，B为三角载波幅值。

DSP的定时器工作在连续增减计数模式，设当定时器工作在增计数模式时三角波的斜率为k1，由图3c及两点直线方程可知：

设正弦调制波ur的函数为yr=sinωt，um的函数为ym=-sinωt。将t1，t2及在该时刻的函数值代入式(1)得到：

当开关频率很高时，可认为sinωt1≈sinωt2≈sin(ωTc／4)，则得到周波变换器开关管第1个高频脉冲宽度为：

式中：T／4=(t1+t2)／2；M为调制比，M=A／B。

当DSP的定时器工作在减计数模式时，设三角波的斜率为k2，同理得到：

当开关频率很高时，可认为sinωt3≈sinωt4≈sin(3ωTc／4)，则得到周波变换器开关管第2个高频脉冲宽度为：

当载波比为偶数时，设载波比为2N，则周波变换器开关管的第n个高频脉冲的宽度为：

根据以上对全桥移相PWM的原理分析，可以设计其实现的软件和控制系统。

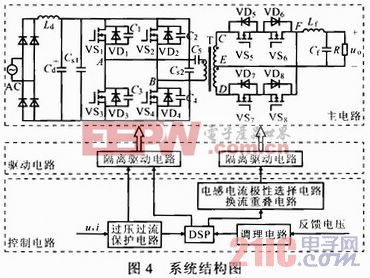
基于DSP的双极性双调制波高频链逆变器的系统如图4所示。DSP芯片为TMS320F2812。系统实现了双极性双调制波控制算法的程序，生成脉冲触发信号，建立了正弦数据表，采用增量式PI算法完成了闭环控制算法。

4 仿真与实验结果

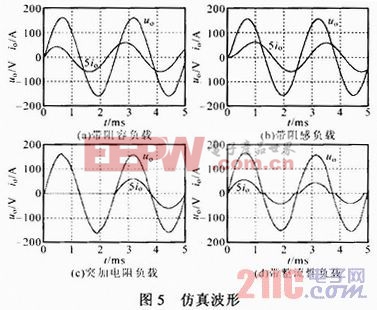
基于上述理论分析和系统设计，通过仿真和实验对方案进行了验证。仿真参数：输入直流电压30 V，高频变压器变比38：34：34，输出滤波电感1 mH，滤波电容4．4μF，开关频率40 kHz，电阻负载，输出电压为400 Hz。LC滤波器前端的电压为双极性SPWM波，经滤波后输出正弦波。在单闭环控制下，高频链逆变器分别带阻容、阻感负载、突加电阻负载及带整流性负载时的输出电压uo、电流io波形如图5所示。系统空载时，uo的峰值处稍有畸变；带整流性负载时uo在第1个周期没有达到稳定，且波形的正弦度略差。但系统带电阻、阻容、阻感负载时，uo波动小，波形正弦度较高，总而言之，该高频链逆变器具有良好的带载能力。