线性预测滤波器在抗多窄带干扰中的应用
加入技术交流群
2 线性预测滤波器在抗窄带干扰中的应用
2．1 线性预测滤波器的抗干扰特性研究
为了更好地阐述自适应线性预测滤波器的抗干扰特性。假设一带宽为20 MHz，信噪比为-32 dB的某扩频系统，信号带内出现了3个很强的点频干扰，每个干扰的干信比都在57 dB，采用16阶前后向的横向预测滤波器，抗干扰前后信号频谱如图2所示。本文引用地址：https://www.eepw.com.cn/article/186153.htm
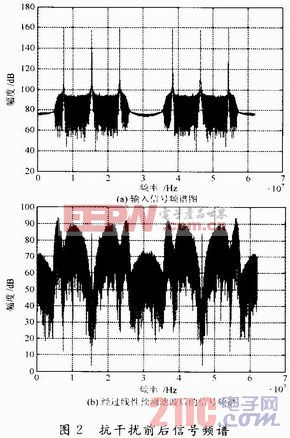
从滤波前后的频谱卜看，对于3个较强的点频干扰滤除较为彻底，在每个干扰位置处都产生了较深的陷波，较好地滤除了干扰，获得干扰抑制增益为60．23 dB，输出信噪比损失仅为1．9 dB，且当横向滤波器的阶数越高，预测的最佳抽头系数能够更加准确地重构出窄带干扰，获得的干扰抑制增益也就越高，当然付出的工程实现代价也随着增大。
2．2 符号LMS递归求解实现
从式(5)可以知道，求解维纳-霍夫方程的解涉及到矩阵求逆，而对于高达16阶的矩阵求逆，工程实现的难度可想而知，因此工程上大多采用LMS，RLS等自适应算法来递归求解，LMS算法由于其工程实现难度小，鲁棒性好的特点而得到广泛应用，在这里采用LMS算法。
LMS算法的统一形式如下：
w(n+1)=w(n)-μ(n)(n) (6)
式中：w(n+1)为第n+1次更新的滤波器系数；(n)为第n次迭代的梯度，通常用适当的估计值
代替，若用
=-2e(n)u(n)代替梯度的无记忆逼近，式中误差信号e(n)为期望输出d(n)与滤波器实际输出之间的误差，得到抽头系数的更新式子如式(7)所示：
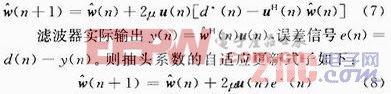
这里需要说明的是，在线性预测滤波器中，输出yi=xi-WTXi，d(n)为窄带干扰信号，扩频信号与噪声与d(n)相互独立，通过LMS重构的是接近于窄带干扰信号的d(n)，而不是能够重构出你想要的扩频信号，抗干扰完成是通过在实际系统中减去通过LMS迭代重构的窄带干扰信号而实现的。
工程实现中LMS的自适应滤波器算法复杂度比较高，一个M阶的滤波器在一个递归更新权值间隔内不仅要完成M次乘法滤波，还需要2M次乘法完成系数更新，这对于设计高阶自适应滤波器来说，对FPGA乘法器资源要求较高，因此采用符号LMS算法显得非常有必要。
评论