基于DSP的混合型有源电力滤波器

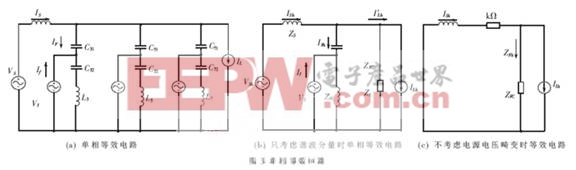
从(6)式可以看出,当ILh、USh为定值时,如果K增大,ISh将减小。当K值足够大时,大部分负载谐波将流入无源滤波器,达到了很好的滤波效果。而且,当不考虑系统电压畸变引起的谐波电流时,即USh=0时,从式(7)可以看出,对于ISh而言,图3(a)和图3(c)是等效的。由图3(c)可以看出,这相当于在电网支路中串联了一个纯电阻K,因此,必然有更多的谐波电流流入无源滤波器。如果K>>|ZFC|,则由负载产生的谐波电流将流入LC滤波器;如果K>>|Z′S|,则滤波特性由K决定。此外,K还起到阻尼Z′S和ZF并联谐振的作用。
2.1 谐波及无功电流的检测
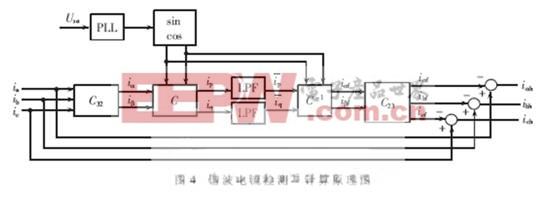
一般电网电流的组成可描述如下:

式中,ispf为瞬时基波有功电流;isqf为瞬时基波无功电流;ish为瞬时总谐波电流。除ispf外,isqf和ish应设法消除。如果能检测出is和ispf,则isqf与ish之和可以由isqf+ish=is-ispf算出[3]。
按照瞬时无功功率理论,ip、iq和三相电流ia、ib、ic有如下关系:

经低通滤波器后得到基波电流ipf、iqf,经过逆运算得出三相基波电流iaf、ibf、icf:

再与ia,ib,ic相减,即可得到谐波电流iah、ibh、ich。其算法原理如图4所示。
图中,
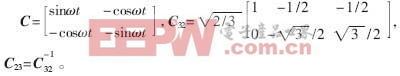
同时检测出谐波和无功时,只需断开图4中计算iq的通道即可。这样,由ipf就可计算出iapf、ibpf、icpf,进而计算出ia、ib、ic的谐波分量和基波无功分量之和iad、ibd、icd[2]。
2.2 控制系统的硬件组成及原理













评论