数字降噪耳机中自适应滤波器的设计实现

　　3 自适应算法

　　自适应滤波器除包括按照某种结构设计的数字滤波器外，还有一套自适应的算法。自适应算法是根据某种判断来设计滤波器的，其目标是使某一特定的函数最小化。自适应算法的种类很多，根据其优化准则的不同可分为两类最基本的算法：最小均方误差(LMS)算法和递推最小二乘(RLS)算法。本文采用最常用的著名的最小均方误差算法，即LMS 算法，这是由Widrow 和Hoff 提出的，是一种易于实现、性能稳健、应用广泛的算法，其目标是通过调整系数，使输出误差序列的均方值最小化，并且根据这个判据来修改权系数。LMS 滤波算法写成矩阵的形式为：

　　式中，W(n)为n 时刻自适应滤波器的权矢量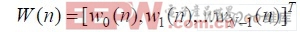；，N 为自适应滤波器的阶数； X(n)为n 时刻自适应滤波器的参考输入矢量，由最近N 个信号采样值构成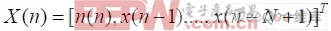，。d (n)是期望的输出值；e(n)为自适应滤波器的输出误差调节信号(简称失调信号)；μ 是控制自适应速度与稳定性的增益常数，又叫收敛因子或步长因子。

　　　4 MATLAB 建模及仿真分析

　　数字降噪耳机可以在很多场合将音频信号中包含的外界环境噪声进行噪声消除。一个标准音频信号往往包含着许多外界环境中的噪音，而由于噪音的随机性和不可预测性，使得所期望得到的信号不再是周期性的标准信号。使用LMS 算法的自适应滤波器能够自适应的进行信号分离，分离出信号中的噪声成分，然后对其反相产生抵消噪声的降噪信号与噪声信号对消，以达到去掉噪声的目的。下面用MATLAB 中的Simulink 工具对数字降噪耳机中DSP 降噪模块自适应滤波器进行建模并仿真。在建模过程中为了确保噪声的相关性，首先让噪声通过了一个低通FIR 滤波器，然后再将其与标准音频信号混合输入到LMS 自适应滤波器中，MATLAB/Simulink 仿真模型中标准音频信号采用频率0.05Hz 的正弦波，噪声信号为随机信号。MATLAB/Simulink 仿真模型如图2 所示。将噪声信号及音频信号输入到数字降噪自适应滤波器之后将产生输出信号和降噪信号，输出信号为自适应的跟踪音频信号，而降噪信号就可以把环境中的噪声信号抵消掉，人的耳朵接收到的信号则变成较纯净的音频信号。

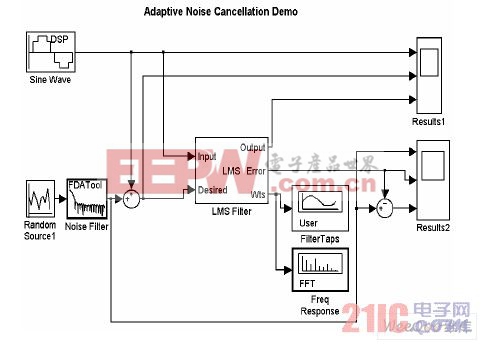
图 2 Simulink 中自适应滤波器仿真