基于人工神经网络的过闸流量软测量研究

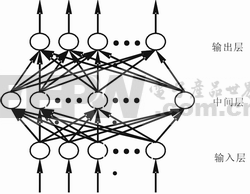
　　由于系统是非线性的，初始值对于学习是否达到局部最小、是否能够收敛以及训练时间的长短的关系很大。一般选取初始权值为(-1，1)之间的随机数。在MATLAB工具箱中可采用函数initnw.m初始化隐含层权值。学习速率决定每一次循环训练中所产生的权值变化量。若学习速率过大可能导致系统的不稳定;但学习速率过小会导致训练时间较长，收敛速度很慢，不过能保证网络的误差值不跳出误差表面的低谷而最终趋于最小误差值。所以在一般情况下，倾向于选取较小的学习速率以保证系统的稳定性。学习速率的选取范围在0.01到0.8之间。综合考虑一下，本系统选取学习速率为0.1。BP网络训练程序如下所示^[9]：

　　%定义输入向量和目标向量

　　P=[0.5 0.6 0.8 ……;0.7082 0.7081 0.7079 ……];
　　T=[0.3744 0.4533 0.3735 0.648 ……];

　　%创建BP网络和定义训练函数及参数

　　net=newcf( minmax(P),[15,1],{‘logsig’,‘purelin’},‘traingd’);
　　net=initnw(net,1);
　　net.trainParam.epochs=5000;
　　net.trainParam.lr=0.1;
　　net.trainParam.goal=0.00001;

　　%训练神经网络

　　[net,tr]=train(net,P,T);

　　待网络训练好后，利用选定的20组测试样本对其进行测试，以测量其泛化能力。测试结果如图2和图3所示。

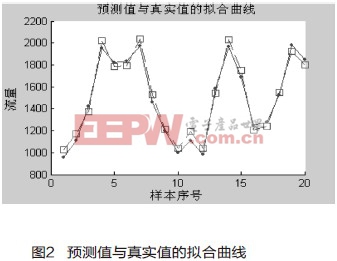
　　图2为真实流量值与通过BP网络软测量模型的预测值之间的拟合曲线，方框代表预测值，圆点代表真实值。

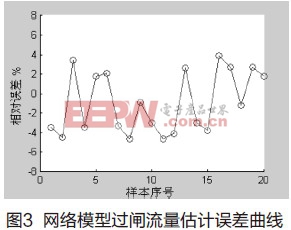
　　图3为BP网络模型过闸流量估计误差曲线，从图中可以看出网络估计误差在5%以内，与流量真值符合良好，反映了软测量模型良好的测量能力。通过改变网络结构、神经元的激活函数、学习算法，进一步增强神经网络对模糊数据的识别能力和容错性，从而可进一步提高模型精度。

　　结论

　　本文提出了一个基于两层BP网络的过闸流量软测量模型，训练与测试结果表明：该网络对过闸流量有很好的预测性，误差在5%以内。而一般传统的流速仪测流的误差也为5%，因此该模型能满足工程测量的需要。另外，预测值与流量真值具有较好的一致性，也充分显示了人工神经网络解决工程问题的适用性。因此，可以通过基于人工神经网络的软测量模型来解决过闸流量与各影响因素之间的复杂非线性关系，为过闸流量的测量提供了一种可供选择的有效手段。

　　参考文献：

　　[1] 穆祥鹏,陈文学,崔巍等.弧形闸门流量计算方法的比较与分析[J].南水北调与水利科技,2009,7(5):20-22
　　[2] 王知生,杨艳玲,王广森.海日苏拦河闸过闸流量的测验方法[J].内蒙古科技与经济,2002,7:72
　　[3] 王孝红,刘文光,于宏亮.工业过程软测量研究[J].济南大学学报(自然科学版),2009,23(1):80-85.
　　[4] 姜万录,雷亚飞,张齐生等.基于神经网络软测量的动态流量测量方法研究[J].流体传动与控制,2007,6:25-30
　　[5] 丛爽.面向MATLAB工具箱的神经网络理论与应用[M].第3版.合肥:中国科学技术大学出版社,2009:65-80
　　[6] 侯媛彬,杜京义,汪梅.神经网络[M].西安:西安电子科技大学出版社,2007:35-39
　　[7] 孙增圻.智能控制理论与技术[M].北京:清华大学出版社,1997:129-134
　　[8] 王峥,王帆.基于神经网络调速系统故障诊断的数学模[J].三峡大学学报(自然科学版),2004,26(2):123-126
　　[9] 周开利 抗药红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社,2005:89-100