中型组机器人运动控制系统的FPGA设计

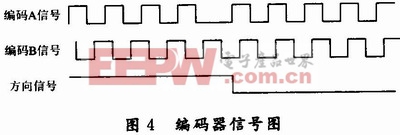
A、B两相信号是相位相差90°的正交方波脉冲串，每个脉冲代表被测对象旋转了一定的角度，A、B之间的相位关系则反映了被测对象的旋转方向。在FPGA中设计4倍频和鉴向电路，本设计采用2路输出：一路输出方向，另一路输出脉冲，并对鉴向倍频电路进行仿真，如图5所示。

根据脉冲计数来测量转速的方法有M法、T法以及M／T法3种。M法适用于高速测量场合，在低速时有较大的误差；而T法，恰恰相反，在低速时测量准确，高速时误差较大。

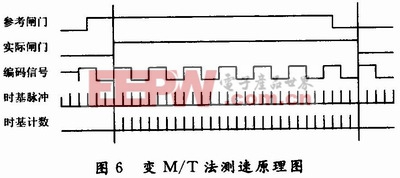
本设计采用文献所描述的方法。该方法如图6所示，设定参考闸门时间为固定的1个值，它只是作为参考信号和编码信号共同确定实际的闸门时间。这样确定的闸门时间为被测信号的整周期倍，能够有效提高测量精度。则测得的速度为：

3．2 增量式PID控制原理及其FPGA实现
实际机器人的数学模型不可避免地存在一定程度的参数不确定性，且三轮全方位移动机器人的正交全向轮在行走时会与地面交替接触而产生一些不确定摩擦转矩，这些都会给机器人的精确控制带来难度。为了对三轮全方位移动机器人进行精确的控制，系统采用PID速度闭环控制算法对机器人的3个全向轮进行速度调节。
令采样周期为TS，将连续PID公式离散化后可得到数字PID算法表达式：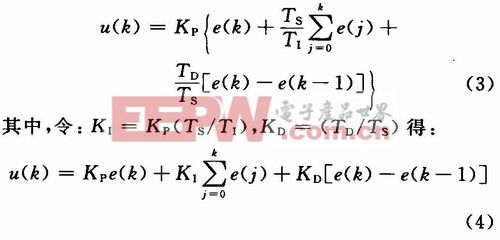


式中：k为采样序号；u(k)为第k个采样时刻的计算机输出值；e(k)为第k个采样时刻的计算机输入误差值；e(k-1)为第k-1个采样时刻的输入误差值；Kp为比例系数；KI为积分系数；KD为微分系数。
这种算法虽然比较直观，但由于是全量输出，所以每次输出均与过去的所有状态有关，计算时要对e(k)进行累加，计算机运算量大。
于是产生了增量式PID算法：



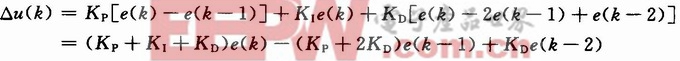
上述公式(7)为增量式PID控制算法。只输出控制增量，误动作影响较小，且控制增量只与最近几次的采样值有关，容易通过加权处理获得比较好的控制效果。
根据以上公式推导，结合FPGA的工作特点，本文设计了适合FPGA的增量式PID实现结构。
由图7可以看出，增量式PID控制算法程序结构，只要最近的3个误差采样值就可以加权计算。这在FPGA内部完全可以并行实现，移位部分结构类似FIR滤波器的实现结构，难点是FPGA设计时对有符号数的熟练操作和保证累加器不能溢出。