基于SPWM 逆变器控制系统的建模与仿真

　　指令传递函数:

　　扰动传递函数:

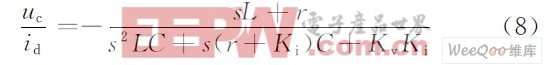
　　2.2 两种控制策略的比较

　　逆变器的输出是对指令响应和扰动响应的和，可以从指令传递函数和扰动传递函数两方面入手，分析比较两种方案的性能。首先通过对指令传递函数和扰动传递函数的bode 图仿真来比较两种方案的动态跟踪性能和扰动抑制能力，从而选择较好的控制方案。

　　在bode 图仿真时，系统参数取基波频率60 Hz ，滤波电感L=1 .1 mH，滤波电容C=20 μF，滤波电感等效电阻r =0.6 Ω，开关频率20 kHz ，选取KV1 =0.2 ，Ki1 =22 ，KV2 =0.2 ，Ki2 =32 。

图6 指令传函的对数幅频响应曲线

　　通过图6 可以比较系统对指令的跟踪效果，可以看到两种方案低频段增益均为1 ，能够完全复现指令，开环逆变器的谐振峰均被消除，具有良好的指令动态跟踪性能。

　　既然逆变器输出是对指令响应和扰动响应的综合，那么只分析逆变器对指令的跟踪效果是不够的，还要考虑对扰动的抑制能力，扰动传函的对数幅频响应曲线就能表征这个能力。

　　通过图7 可以看到，由于扰动主要位于低频段，所以通过这一段的波特图判断扰动抑制性能，低频增益越小，表明系统对扰动的衰减越厉害，即对扰动的抑制效果越好。如图所示，方案一对7 次以下的谐波均有衰减作用，方案二对5 次以下的谐波均有衰减作用，在60 Hz 处，方案一对基波扰动的抑制要好于方案二，这是因为方案二没有实现电感等效电阻解耦，基波在这个电阻上有压降，影响了输出波形。

图7 扰动传函的对数幅频响应曲线

　　通过以上对指令和扰动传递函数的分析可知，两种方案对指令的跟踪能力是很接近的，因此选择方案的主要依据是它们对扰动的抑制能力。方案一通过前馈而方案二通过反馈对扰动进行补偿，考虑到反馈电感电流能够实现电感等效电阻解耦，故方案一在低频段的扰动抑制能力强于方案二，因此，选择方案一作为系统的控制结构。

　　3 系统仿真

　　3 .1 系统仿真模型

　　本文在MATLAB 环境下的Simulink 中建模和仿真。该仿真模型主要分为两个部分:主电路和控制器。主电路如图8 所示，控制器主要由电压电流反馈环节、负载电流补偿环节、SPWM 发生环节和死区延迟环节组成。从主电路仿真模型可以看到:在检验突加、突减非线性负载时，用两个脉冲波、乘法器和理想开关组成矩形脉冲信号，周期为0.4 s ，在0。2 s 时突加额定负载，在0.4 s 时，突减额定负载。系统仿真参数取基波频率为60 Hz ，直流母线电压E=400 V，滤波电感L=1 .1 mH，滤波电容C=20 μF，滤波电感等效电阻r=0.6 Ω，开关频率为20 kHz ，输出电压幅值为220 V，输出额定功率因数cosΦ=0.8 。

图8 主电路仿真模型