基于传感器网络的多目标跟踪和特征管理方法
加入技术交流群
分离的过程如图2所示，其中K为轨迹数量，|Tk|为Tk的基数，当没有轨迹互扰的情况下认为Tk为一个正确的轨迹。假设一条轨迹至少包含两个观测值，因为不能由一个单一的观察值确定一条轨迹。于是再假设e(t-1)为时刻t-1之后目标的数量，z(t)为时刻t消失的目标的数量，c(t)=e(t-1)-z(t)为时刻t-1到t未消失的数量。设a(t)为时刻t新出现的目标，d(t)为时刻t的实际目标，g(t)=c(t)+a(t)-d(t)为未识别的目标。最后，设f(t)=n(t)-d(t)为错误报警数量，有：
其中P(ω|Y)是Y的相似概率。本文引用地址：https://www.eepw.com.cn/article/160284.htm
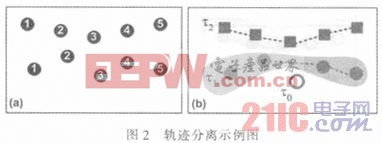
本文采用了最大后验MAP算法解决多目标跟踪问题。该算法对观测目标进行分割，并根据分割对目标状态进行估算。
3 马尔科夫链蒙特卡洛数据融合
本节提出一种解决第二节中多目标跟踪问题的算法，该算法是离散多目标跟踪与识别算法模块的核心。
3．1 马尔科夫链蒙特卡洛模型
马尔科夫链蒙特卡洛模型是已知唯一能在多项式时间复杂问题下实现估值计算的方法，同时，还是一种从位于空间Ω的分布π中提取抽样值的普遍方法，该方法通过状态值ω∈Ω和稳定分布值π(ω)建立的马尔科夫链M来实现其算法。现在来描述该算法。在状态ω∈Ω，假设ω’∈Ω服从分布q(ω，ω’)。而运动的感知服从感知慨率A(ω，ω’)，其中：
然而样本保持在ω。通过计算，平衡条件得以满足，例如，对于所有的ω：
其中，P(ω，ω’)=q(ω，ω’)A(ω，ω’)是从ω到ω’的跃迁概率。
如果M具约束性和非周期性，并且M由遍历定理收敛至均匀分布。因此，对于一个给定的有界函数f：Ω→Rm，样本均值
，其中ωn是M在时刻t的状态，当Eπf(ω)收敛于N→∞。可以注意到公式(4)只需计算出π(ω’)／π(ω)的比值，而无需对π进行标准化。
3．2 马尔科夫链蒙特卡洛数据关联
MCMCDA算法是马尔科夫链蒙特卡洛算法的特殊形式，其状态空间是上文在第2．2节中提到的，并且其平稳分布服从公式(3)。对于MCMCDA的分布有5类动作组成。它们包括：1)发现／消失运动；2)分割／合并运动：3)扩展／减少运动；4)跟踪刷新运动；5)跟踪切换运动。
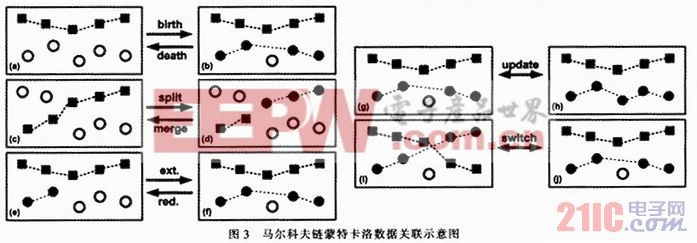
MCMCDA的运动方式如图3中所示，每个运动的详细描述在此省略。MCMCDA的输入是一系列观测值Y，样本观测值的个数nmc，初始状态ωinit，以及有界函数X：Ω→Rm。对于该算法的每一步，ω是马尔科夫链的当前状态。其获取概率A(ω，ω’)如公式(4)，输出
接近MMSE的估计值EπX，且
接近MAP的估计值arg maxP(ω|Y)。
评论