微球激光在极高灵敏度传感器方面的原理及应用

假设一个微粒附着在微球表面附近的ri处(如图1)，根据经典电动力学，微球腔的电场强度分布为E0(ri)exp(iωt)，倏逝场在表面产生电偶极矩为δpexp(iωt)， 于是能量改变为：

hδω=-δpE0*(ri)/2

又有：δp=αexE0(ri)，则：

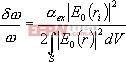
(1)

以上各式中，E0(r)—微球腔中半径为r处的电场强度;

αex—剩余极化强度;ω—电磁场的圆频率;δω—圆频率的变化量;V—体积;t—时间;p—电偶极矩;δp—电偶极矩的变化量;h—普朗克常数。

假设微球外部有N个微粒，则微粒在微球表面附近的表面密度为：

σp=N/4πR2w

近似的，将求和改为积分，即：

根据场论理论有：

(2)

其中，A—面积;k0—波矢;εrs—介质介电常数;jl—一阶球贝塞尔函数;Ylm—球谐函数。

代入(1)式化简并根据近似条件2πR/λ>>1，可以得到该类传感器的灵敏度公式：

(3)

其中，ns、nm—微球与外部环境的折射率;ε0—真空介电常数;R—微球半径。

实验采用了锥形光纤耦合。最基本的耦合方式是棱镜耦合(如图2)，一束光从玻璃达到界面上，当i>ic时，将发生全反射现象。根据电动力学的推导结论，在空气介质方有一个倏逝场。将微球置于该倏逝场的适当位置，使之与微球腔的本征模式相匹配，外部的光就从外界的传播波耦合进入微球，在微球腔中激发出回音壁模式。现在，实验中一般采用锥形光纤实现高效率的耦合。

Vollmer等的实验装置如图3。在溶液中溶解一定浓度的牛血清蛋白，通过微球置于溶液前后光电流的变化来研究这一传感器的精度效果。整个装置的本底电流只有20μA，光电倍增管对波长的探测灵敏度为0.009nm/mA。微球置于溶液中的一开始，光电流突然下降，过一段时间后才逐渐回升并最终增大了大约2mA。光电流上升是预料中的，它已经由公式决定。分析表明，一开始光电流之所以下降，是因为微球置于溶液中的一刻，微球温度减小使波长显著降低，经一定时间的恢复后，光电流达到稳定。这从另一个侧面反映了微球对于外界温度的灵敏反应。

在这个装置下，能够探测到的生物分子的分子量下限为50，是以前一些生物传感器的1/3还少。并且灵敏度公式还表示，即使是生物分子附在微球上原子尺度厚度的层面，微球同样有反应。正如他们所说，这种生物传感器具有“前所未有的精度”。

三、在极高灵敏度加速度传感器上的应用[7]

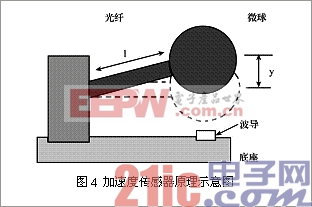
不同于前面的例子，Laine等研究开发的是一种极高灵敏度加速度传感器，该器件是通过微球谐振腔与耦合器件之间的相对距离改变来进行检测的，并且耦合方法不再是锥形光纤，而是一种带状基底抗谐振反射光波导(SPARROW：stripline pedestal anti-resonant reflecting optical waveguide)。它通过交替的高低折射率层组成的介质堆将微球腔、波导与底层隔离开来，使在第一个分界面上的反射率超过99%[5]。该加速度传感器的原理如图4。

球微球球重W，半径为r，与一长为l的光纤杆相连，光纤像一般的弹性材料那样一端固定在基板上，杨氏常数为E，另一端通过化学烧制做成微球(一般通过高温熔融冷却法制成)，在微球下面，SPARROW与它相耦合。近似的，将微球视为质点，光纤杆视为理想杆，因二者振动产生相对于平衡位置的位移为：

(4)

其中，I —细杆的转动惯量;E—杨氏系数;

w—球回复力， ;

w—细杆的回复力，

;

a—系统的加速度。

如果测出了y，我们就可以推出加速度a。但是，由于y的变化很小(nm量级)，所以一般的测量方法已经相形见绌。此时，微球谐振腔就有了用武之地。光波导与微球的相对距离变化可以通过测量微球的品质因子可以得到：

(5)

(6)

其中，Qc(d)—和耦合方式有关的品质因子;Q0—微球腔的本征品质因子，与材料以及半径有关;Q(d)—微球腔的总品质因子;r—微球半径;λ—入射光波波长;n —微球材料的折射率;Q—光波的模式数，一般小于10，指约束在赤道表面的光波模式数目。

通过实验测量品质因子，可推得Qc(d)，从而反解出d，通过d可以计算y值，最终实现测量加速度。

Laine等在实验中采用了多项先进技术，如SPARROW的选用能使光波的渗漏达到最小，微球腔品质因子保持在108以上的较高水平等。通过检测谐振振幅和线宽的改变，从100μg的背景噪音中实现了1mg的极高灵敏度的加速度探测。