高灵敏度微球激光传感器基本原理

假设一个微粒附着在微球表面附近的ri处(如图1)，根据经典电动力学，微球腔的电场强度分布为E0(ri)exp(iωt)，倏逝场在表面产生电偶极矩为δpexp(iωt)， 于是能量改变为：

hδω=-δpE0*(ri)/2

又有：δp=αexE0(ri)，则：

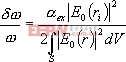
(1)

以上各式中，E0(r)—微球腔中半径为r处的电场强度;

αex—剩余极化强度;ω—电磁场的圆频率;δω—圆频率的变化量;V—体积;t—时间;p—电偶极矩;δp—电偶极矩的变化量;h—普朗克常数。

假设微球外部有N个微粒，则微粒在微球表面附近的表面密度为：

σp=N/4πR2w

近似的，将求和改为积分，即：

根据场论理论有：

(2)

其中，A—面积;k0—波矢;εrs—介质介电常数;jl—一阶球贝塞尔函数;Ylm—球谐函数。

代入(1)式化简并根据近似条件2πR/λ>>1，可以得到该类传感器的灵敏度公式：

(3)

其中，ns、nm—微球与外部环境的折射率;ε0—真空介电常数;R—微球半径。

实验采用了锥形光纤耦合。最基本的耦合方式是棱镜耦合(如图2)，一束光从玻璃达到界面上，当i>ic时，将发生全反射现象。根据电动力学的推导结论，在空气介质方有一个倏逝场。将微球置于该倏逝场的适当位置，使之与微球腔的本征模式相匹配，外部的光就从外界的传播波耦合进入微球，在微球腔中激发出回音壁模式。现在，实验中一般采用锥形光纤实现高效率的耦合。

Vollmer等的实验装置如图3。在溶液中溶解一定浓度的牛血清蛋白，通过微球置于溶液前后光电流的变化来研究这一传感器的精度效果。整个装置的本底电流只有20μA，光电倍增管对波长的探测灵敏度为0.009nm/mA。微球置于溶液中的一开始，光电流突然下降，过一段时间后才逐渐回升并最终增大了大约2mA。光电流上升是预料中的，它已经由公式决定。分析表明，一开始光电流之所以下降，是因为微球置于溶液中的一刻，微球温度减小使波长显著降低，经一定时间的恢复后，光电流达到稳定。这从另一个侧面反映了微球对于外界温度的灵敏反应。

在这个装置下，能够探测到的生物分子的分子量下限为50，是以前一些生物传感器的1/3还少。并且灵敏度公式还表示，即使是生物分子附在微球上原子尺度厚度的层面，微球同样有反应。正如他们所说，这种生物传感器具有“前所未有的精度”。