了解环形调制器如何产生AM信号

在调制器电路中，环形调制器是产生AM信号最有效的调制器之一。在本文中了解原因。

调幅（AM）信号可以使用几种类型的调制器电路产生。例如，开关调制器将消息信号乘以基频等于所需载波频率的周期函数。这会产生基频及其谐波的AM波。然后，带通滤波器将所需的频谱分量传递到输出端。

我们在前一篇文章中了解了开关调制器家族的一个成员，二极管桥调制器。在本文中，我们将深入研究一种不同的、性能更高的开关调制器电路：环形调制器。

二极管桥式调制器综述

在继续之前，让我们重新审视二极管桥调制器的关键方面。这将有助于我们更好地理解环形调制器的微妙之处，以及它比二极管桥调制器提供的性能改进。

使用二极管桥式调制器，消息信号（m（t））乘以在零和一之间切换的方波（g（t）。如图1所示。

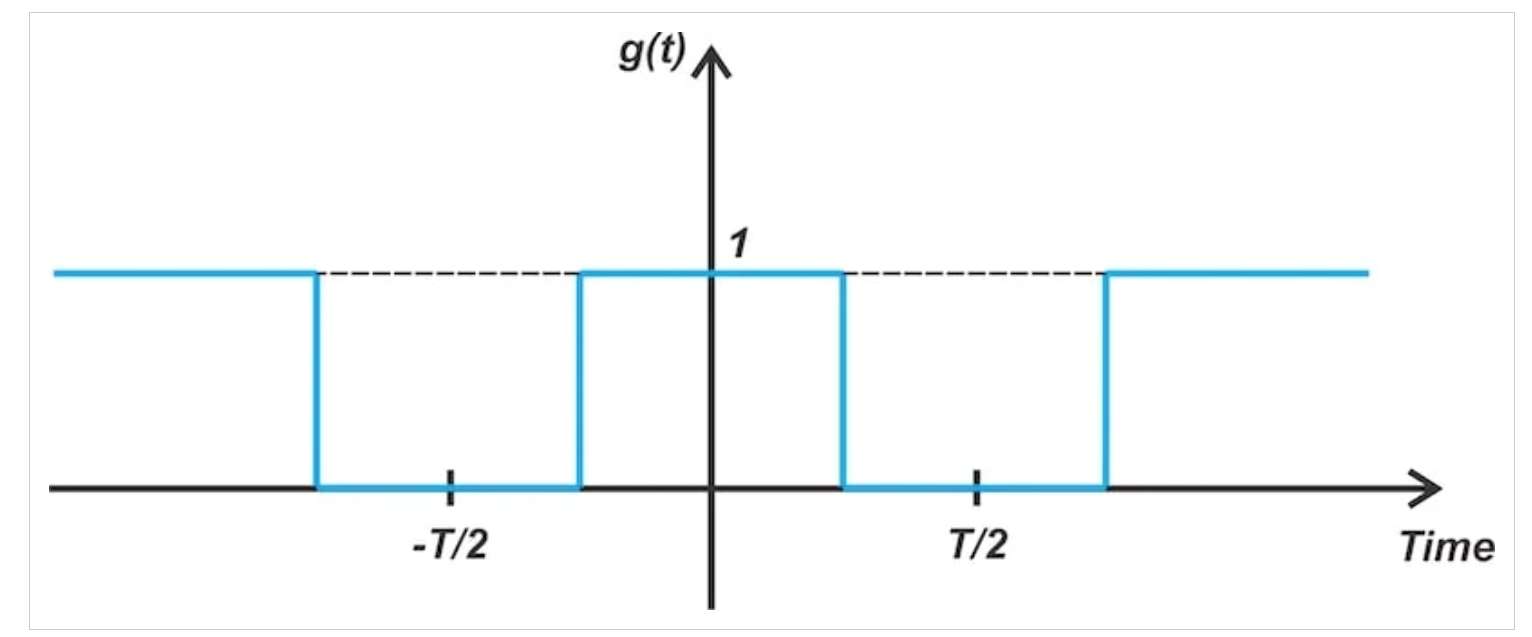
图1 二极管桥式调制器中的门控功能

假设消息信号是单音正弦波，乘以方波会产生图2中的蓝色波形。

通过带通滤波器前后的输出信号。

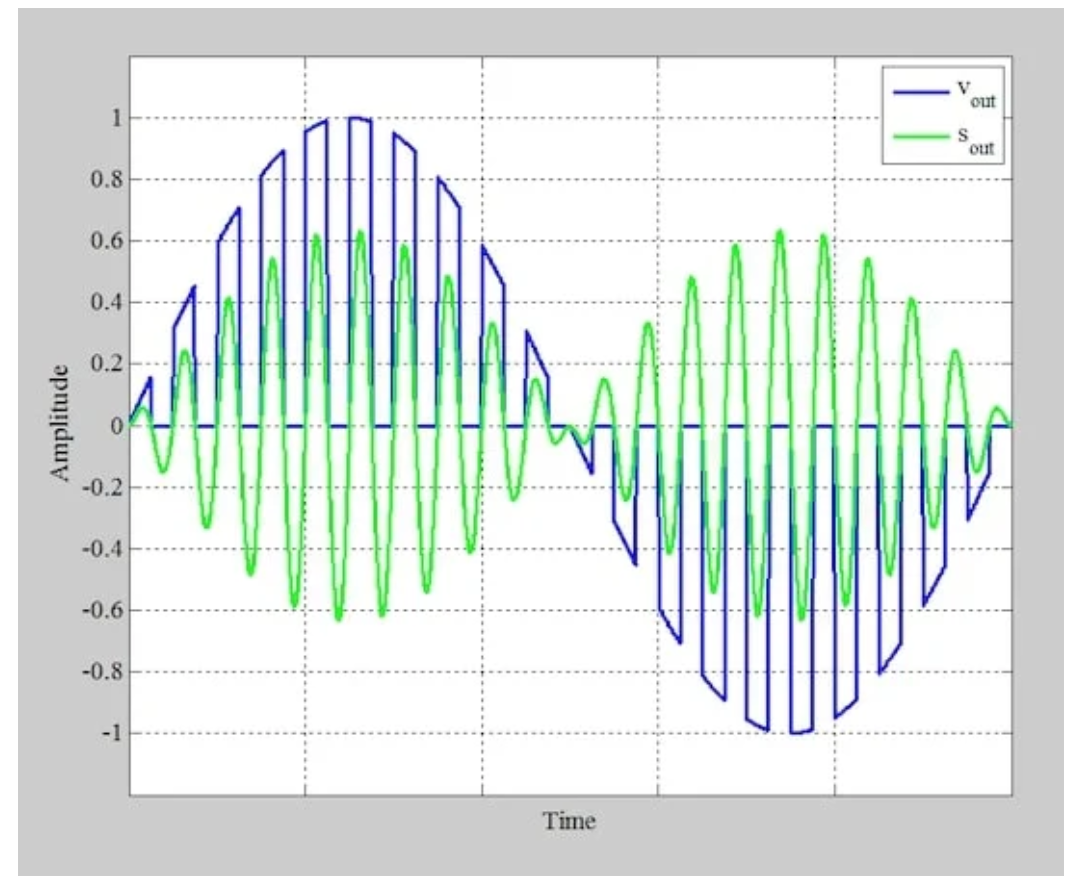
图2 应用门控功能后的信号（蓝色）和带通滤波器输出端的结果信号（绿色）

为了产生最终的AM波，我们需要将蓝色波形通过调谐到载波频率（fc）的带通滤波器。这生成了上图中的绿色波形。

数学分析表明，滤波器输出端的最终信号由下式给出：

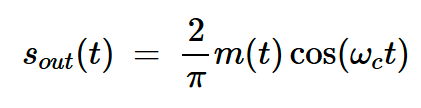
方程式1

在频域中，乘以图1所示的方波会产生以0、±fc、±3fc、±5fc等为中心的消息信号频谱的副本，如图3所示。

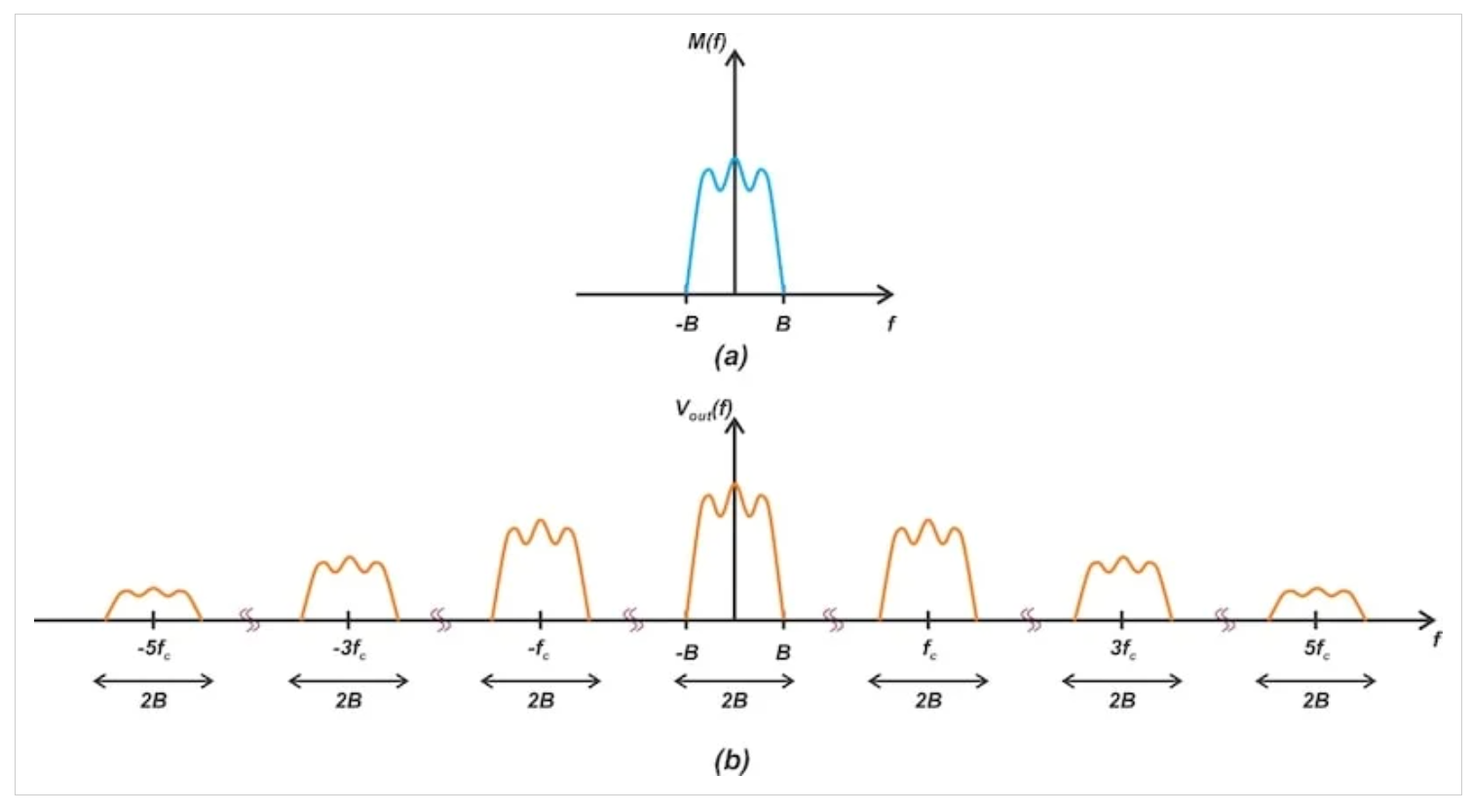
图3 基带消息信号（a）的频谱和在应用带通滤波器（b）之前由调制器产生的信号

现在我们已经回顾了二极管桥式调制器，让我们来探索一下环形调制器。

环形调制器的操作

图4显示了环形调制器的电路示意图。它使用四个二极管，它们以形成一个回路的方式排列——这种配置就是以“环”命名的。

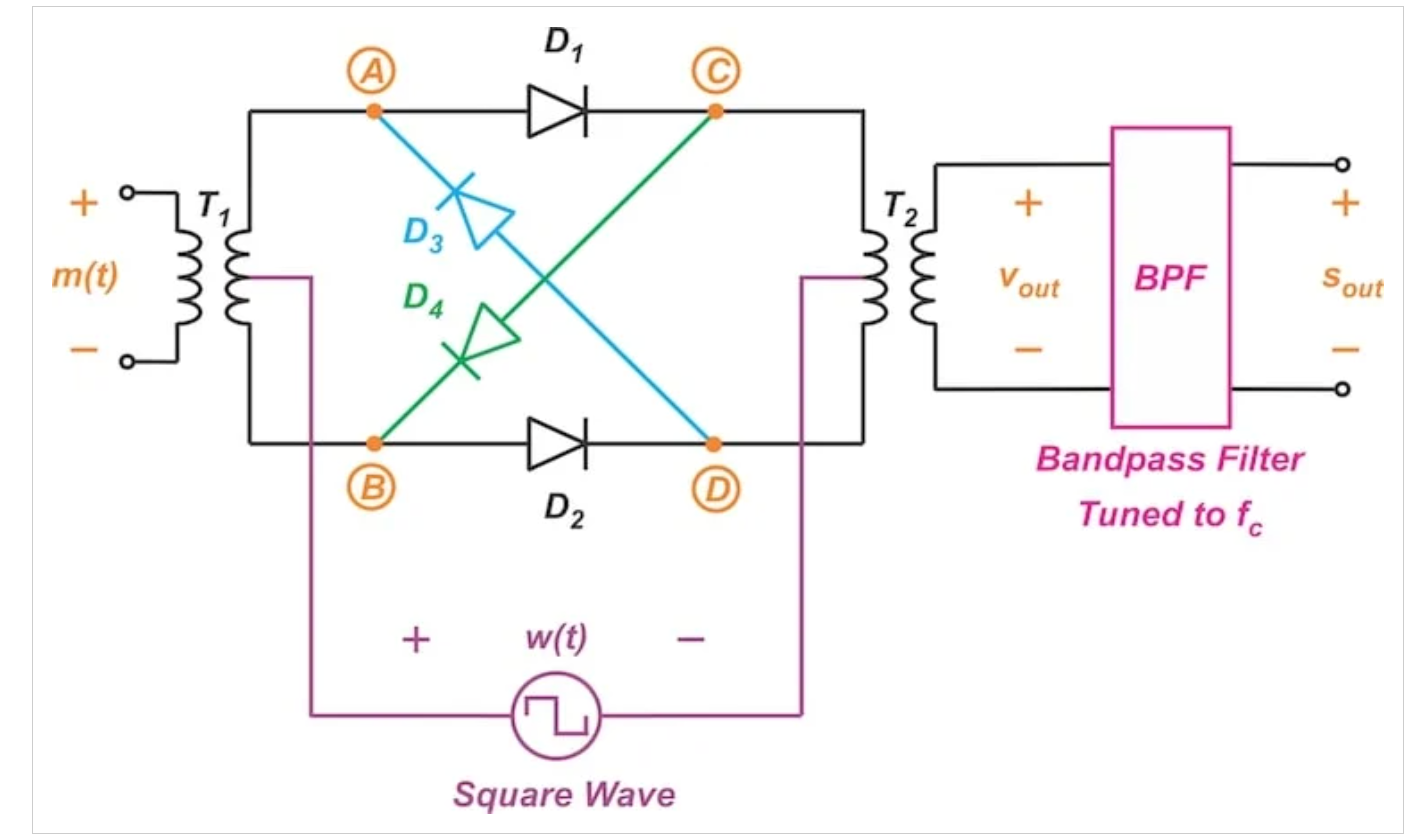
图4 环形调制器示意图

在图4的底部，我们看到一个方波（w（t））。该方波的振幅为±A1，被馈入变压器（T1和T2）的中心抽头，并以基频（fc）切换。

当w（t）为大正值时，以下情况成立：

二极管D1和D2接通。

横臂部分（D3和D4）中的二极管关闭。

节点A连接到节点C。

节点B连接到节点D。

换句话说，在w（t）的正半周期内，T1次级两端的电压以其原始极性传输到T2初级。

当w（t）为大负值时：

二极管D3和D4接通。

二极管D1和D2断开。

节点A连接到节点D。

节点B连接到节点C。

因此，在负半周期内，T1次级两端的电压以相反的极性传输到T2初级。

实际上，环形调制器充当换向器，周期性地反转电压方向。从数学上讲，消息信号乘以在±1之间切换的方波。如图5所示。

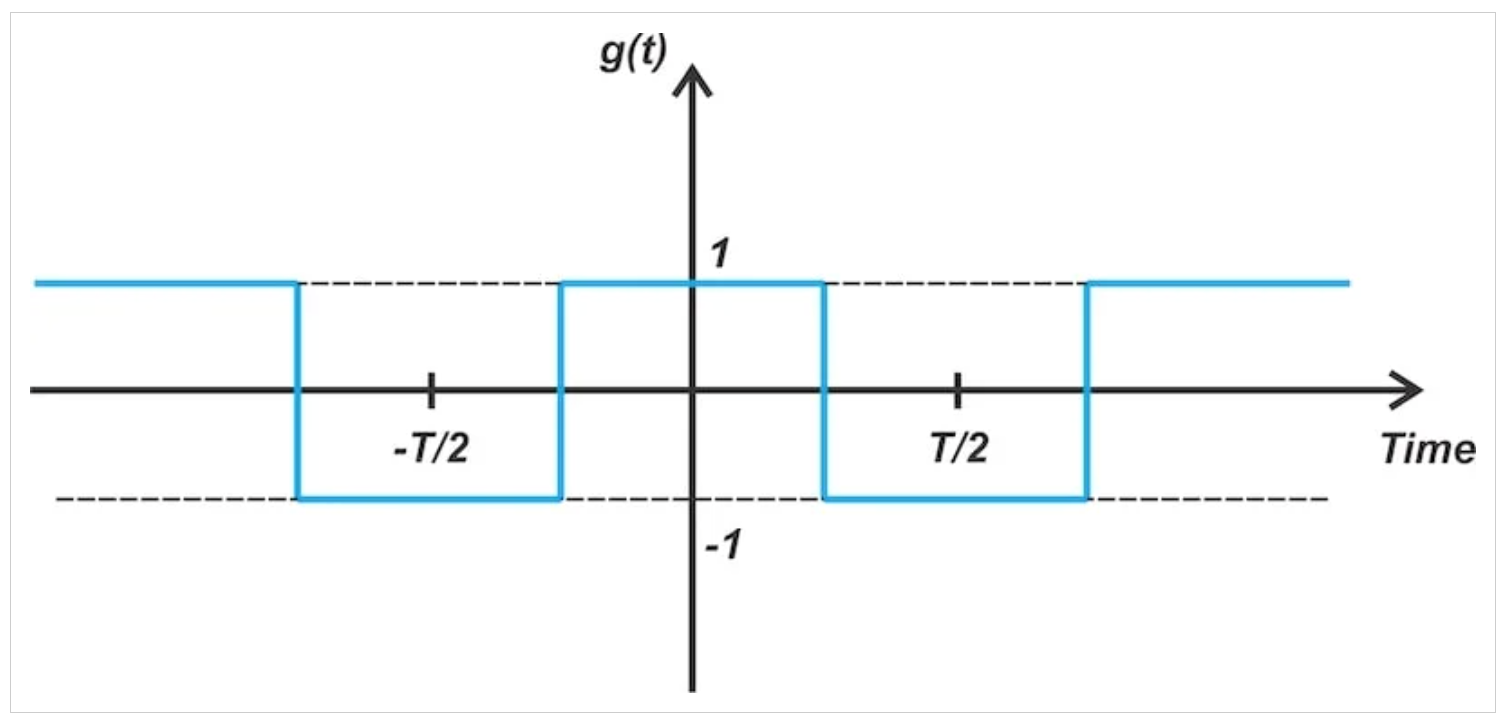
图5 环形调制器中使用的门控功能

接下来，让我们考虑这个电路的时域波形。

时域波形

与二极管桥调制器一样，我们通过向电路施加单音正弦消息信号来检查时域行为。图6的上图显示了消息信号；下图显示了由于电路操作而乘以m（t）的波形。

施加到环形调制器的单音输入（顶部）和有效倍增消息的波形（底部）。

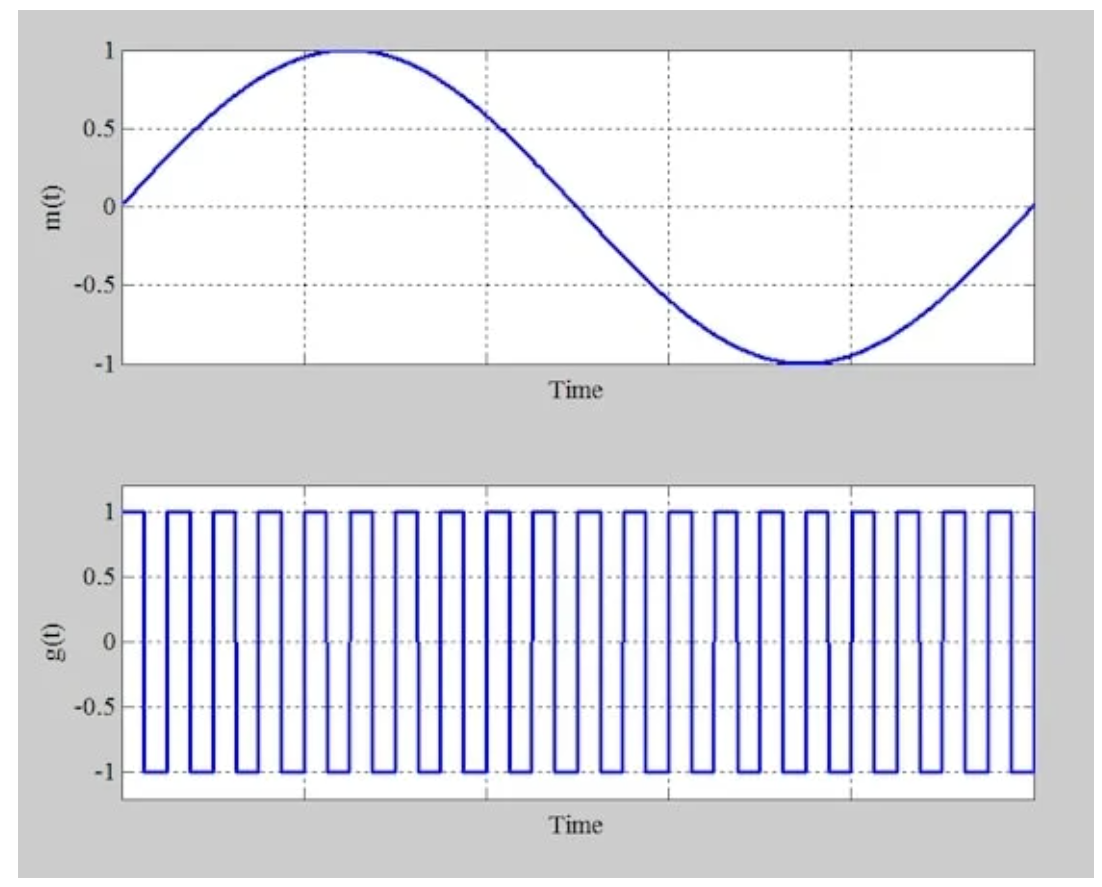
图6 施加到环形调制器的单音输入（顶部）和有效倍增消息的波形（底部）

我们假设两个变压器的匝数比为1，所有二极管的电压降为零。

图7显示了将这些波形相乘得到的输出电压（vout）。

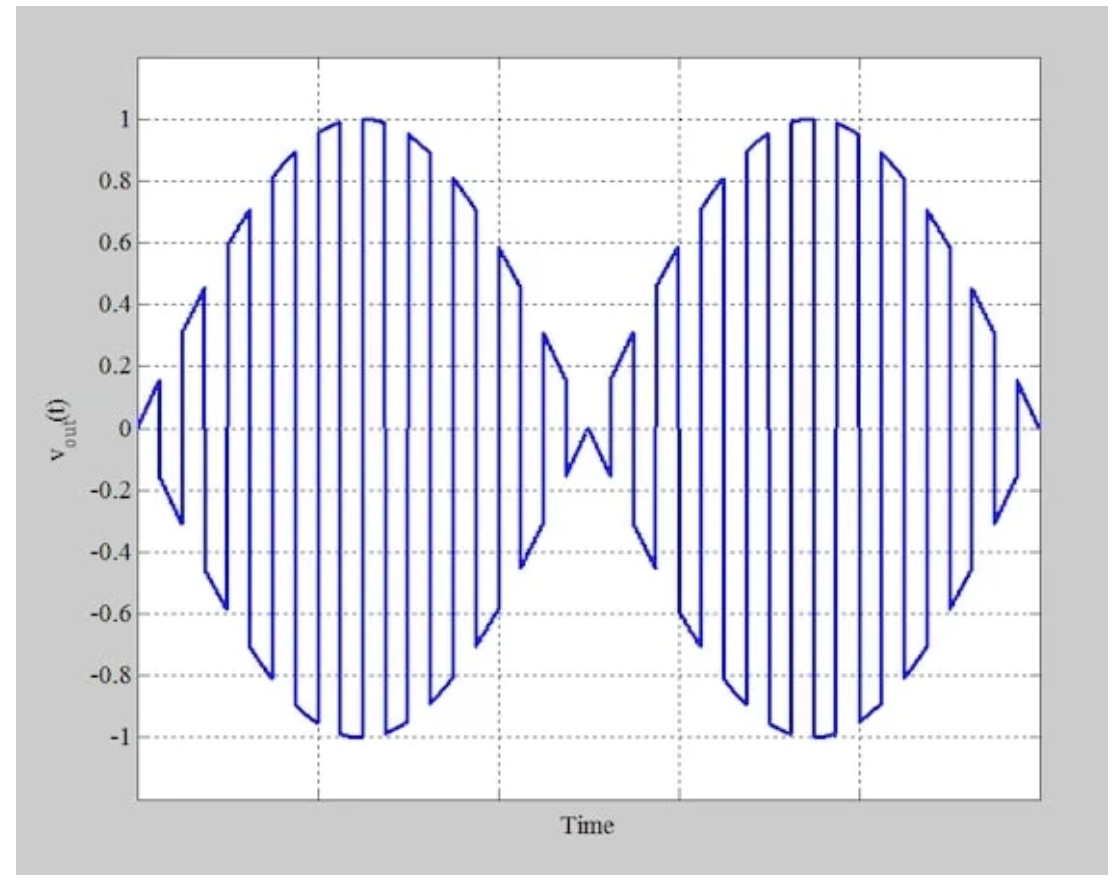
图7 环形调制器产生的输出波形（vout）

与二极管桥式调制器一样，环形调制器要求我们通过带通滤波器来产生最终的AM波。应用适当的带通滤波器会产生图8中的绿色波形。

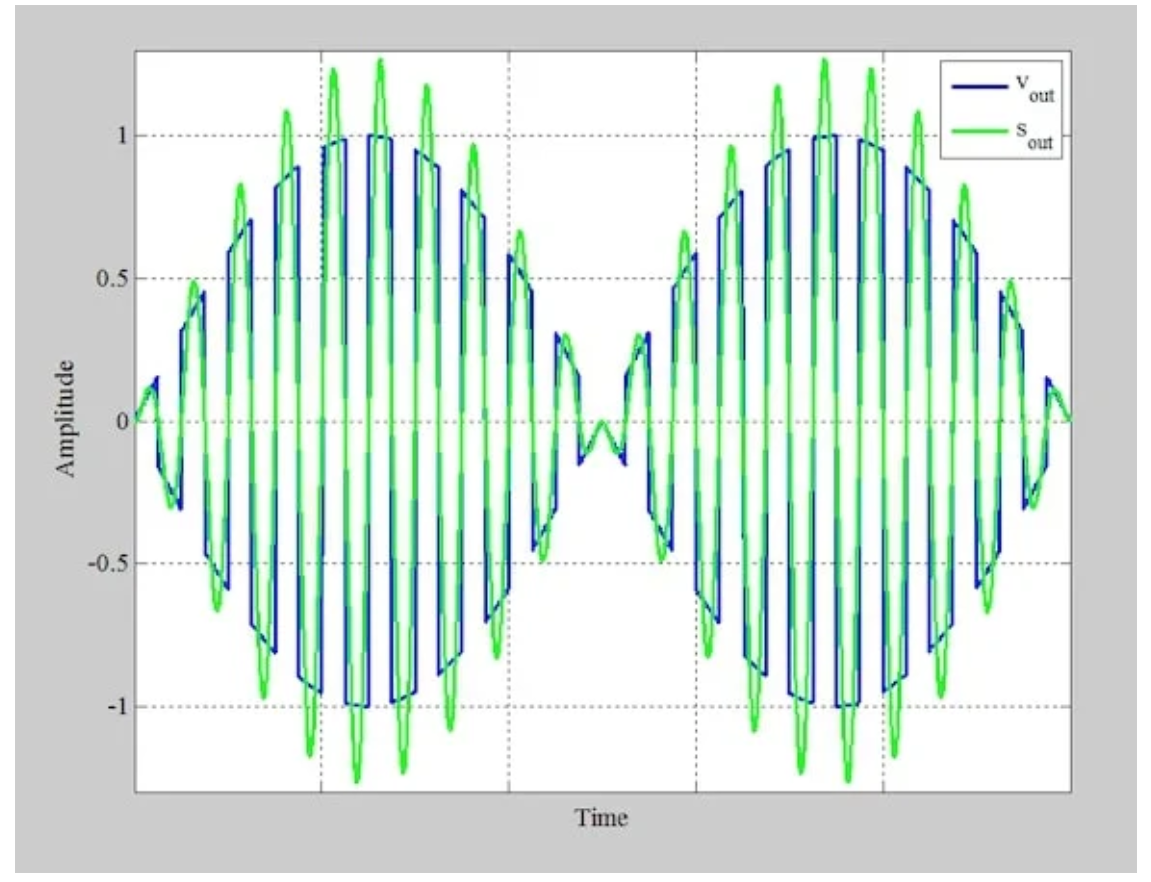
图8 应用门控功能后的信号（蓝色）和带通滤波器输出端的最终信号（绿色）

推导输出信号方程

为了推导输出信号的方程，我们注意到图5（g（t））中描绘的门控函数可以用以下傅里叶级数展开式表示：

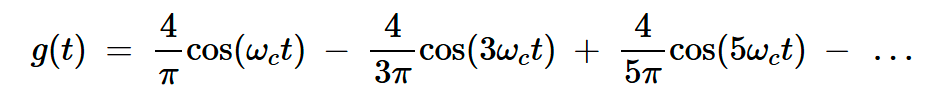
方程式2

注意，由于g（t）是偶数函数，因此它只能用余弦函数展开。输出电压为：

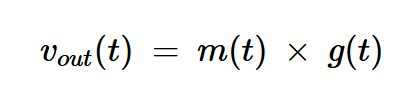
方程式3

结合上述方程式得出：

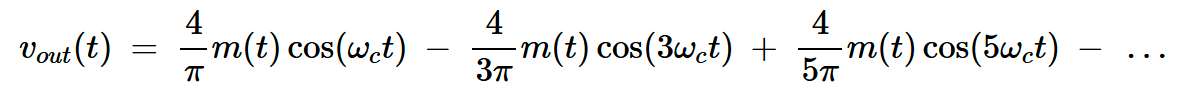
方程式4

方程4表明，vout（t）是以c、±3 c、±5 c等为中心的AM波的叠加。如图9所示。

基带消息信号（a）的频谱和在应用带通滤波器（b）之前由环形调制器产生的信号。

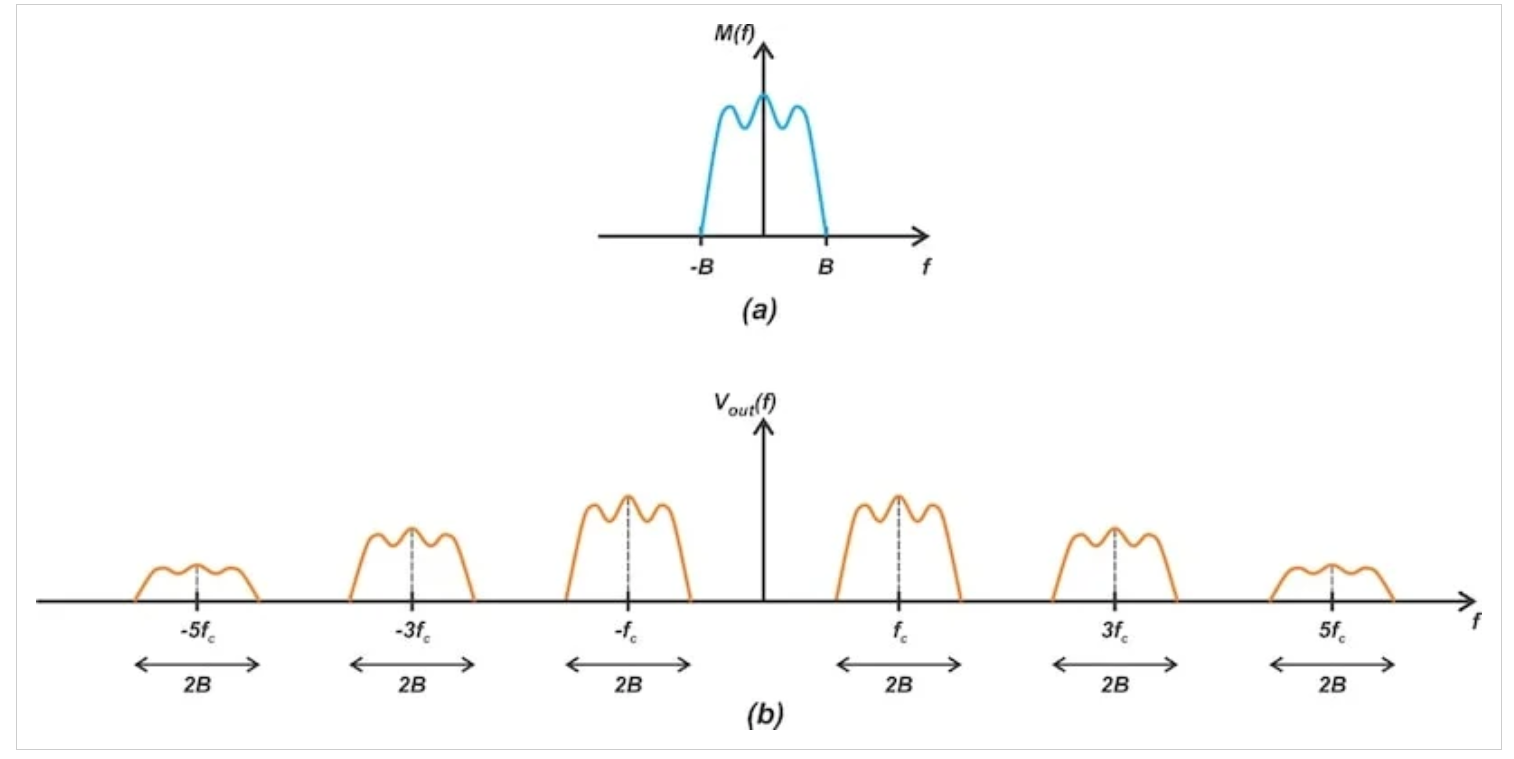
图9 基带消息信号（a）的频谱和在应用带通滤波器（b）之前由环形调制器产生的信号

该电路抑制载波，同时保留实际传输信息的边带。正如我们将在文章的最后谈到的那样，在使用环形调制器时也可以保留载波。然而，这在很大程度上超出了本次讨论的范围。

回到图9，所需的频谱以fc为中心。为了将其与其他频谱成分分开，我们应该：

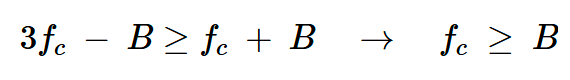
方程式5

这种情况在实践中很容易实现，因为载波频率与基带信号带宽的比率（fc/B）通常在100到300之间。

为了选择±fc附近的所需边带，环形调制器包括一个带通滤波器。使用理想的带通滤波器，只有以fc为中心的频谱分量才能通过输出，导致：

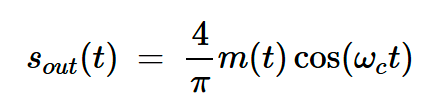
方程式6

二极管电桥与环形调制器的比较

现在我们已经研究了环形调制器的电路、波形和方程，让我们讨论一下它与二极管桥调制器之间的一些重要区别。

门控功能的直流分量

二极管桥调制器的门控功能的直流值为0.5。如图3所示，将消息信号乘以此门控函数会创建零频率附近m（t）频谱的副本。为了抑制这种频谱分量，二极管桥调制器的滤波器应该具有（fc-B）-B≈fc的过渡带。

另一方面，环形调制器的门控功能没有直流分量。因此，我们在图9中看到，在输出端的零频率附近没有出现频谱分量。相反，最接近的光谱分量集中在3fc处。

这会影响带通滤波器过渡带的锐度。为了抑制以3fc为中心的频谱分量，环形调制器需要一个过渡带为|（fc+B）−（3fc-B）|≈2fc的滤波器。

时域波形的对称性

要了解环形调制器如何消除以f=0为中心的频谱分量，请考虑其时域波形。检查这些波形，我们看到环形调制器在滤波器输入端产生的信号关于零对称。这种对称性消除了零频率（DC）下的消息信号频谱。

这种对称性之所以出现，是因为环形调制器在交替的半周期内输出具有原始或反转极性的消息信号。相比之下，二极管桥调制器产生的信号在半个周期内等于消息信号，在另一个周期内降至零。

双平衡与单平衡

在带通滤波器的输入端，环形调制器仅产生乘积项。它抑制了消息和载波信号。因为它抵消了基带信号和载波，所以我们称环形调制器为双平衡。

另一方面，二极管桥调制器仅相对于载波输入保持平衡。消息信号出现在带通滤波器的输入端，使其成为一个单平衡调制器。

输出电压电平

比较方程1和6，我们观察到环形调制器产生的输出电压是二极管桥式调制器的两倍。这与图2和图8所示的绿色波形一致。这些图分别显示了最大振幅为0.63和1.26的AM波。

总结

环形调制器在一个半周期内以原始极性将输入信号传输到输出端，在交替的半周期内则以相反的极性传输。这放宽了带通滤波器的过渡带要求，并使输出信号的幅度加倍。应该指出的是，防止载波功率泄漏到环形调制器的输出中需要完全平衡的变压器和匹配的二极管。

另外，环形调制器还可以用于产生不抑制载波的AM信号。为了理解如何，我们注意到环形调制器有效地充当了乘法器。由于对输入消息信号没有限制，我们可以通过向环形调制器施加具有任意调制指数的1+μm（t）来产生传统的AM信号。