开关调制器如何产生AM信号？

以二极管桥调制器为例，我们研究了用于AM信号生成的开关调制器的基本原理。

线性时不变（LTI）系统不能产生输入信号中存在的频率以外的频率。由于调制将输入频率转移到输出端的不同范围，因此需要非线性、时变或两者兼具的电路。因此，许多主要从事LTI系统分析和设计的电气工程师可能不太熟悉调制器电路。

为了帮助纠正这一知识差距，本系列之前的文章介绍了平方律调制器和平衡调制器的基础知识。这两者都是基于乘法器的电路。在本文中，我们将简要回顾基于乘法器的调制器，然后将注意力转向开关调制器。我们将以在MATLAB中模拟带通滤波器的一些指导来结束我们的讨论。

调制方法与乘法器综述

到目前为止，在本系列中，我们讨论了两种类型的调幅（AM）：

双边带抑制载波（DSB-SC）调制。

常规AM。

使用DSB-SC调制，调制信号s（t）是通过将消息信号m（t）乘以正弦载波c（t）=Accos（ωct）而产生的：

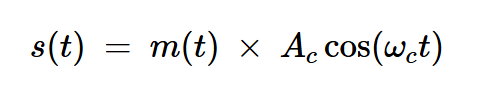
方程式1

在传输频谱中保留载波的传统AM使用以下方程式：

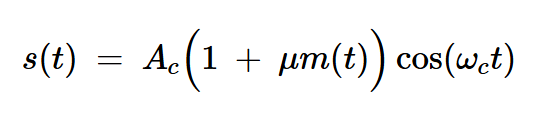
方程式2

我们可以使用模拟乘法器直接计算由方程1和2描述的输出信号。例如，图1说明了生成传统AM信号的两种可能配置。

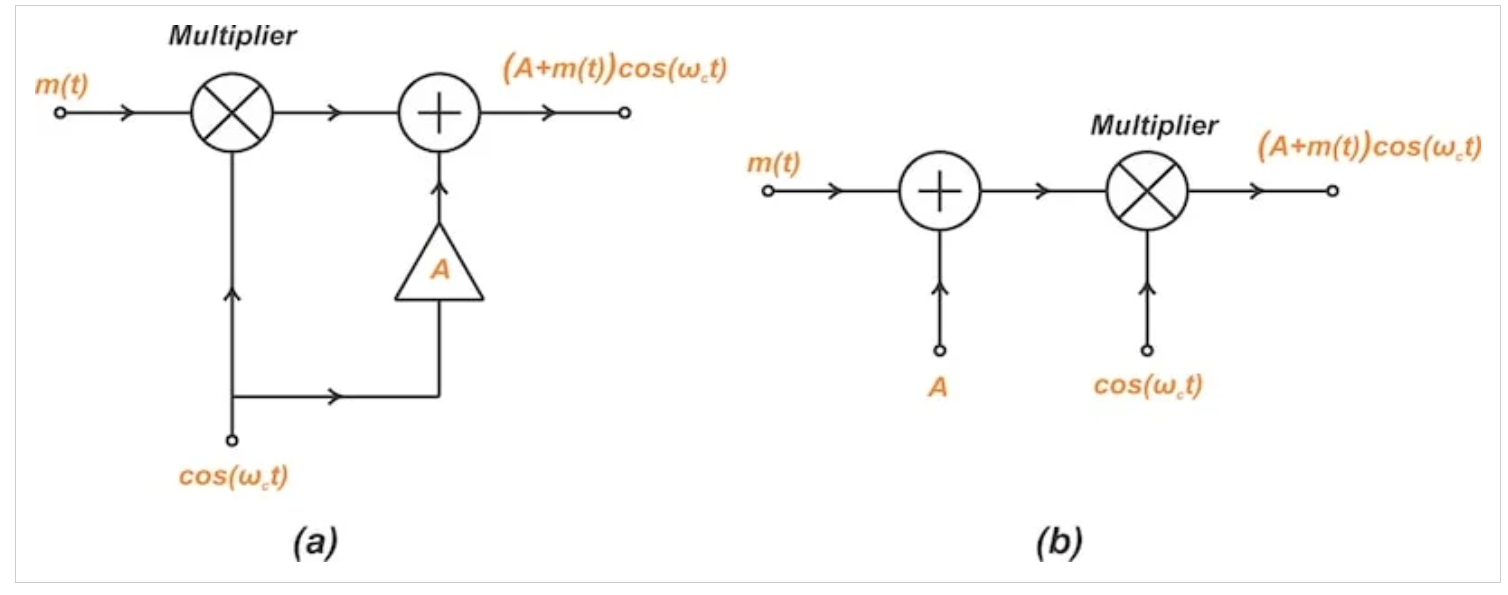
图1产生传统AM波的两种可能安排

我们可以使用吉尔伯特单元、霍尔效应器件或对数/反对数放大器来实现模拟乘法。然而，大多数模拟乘法器在低功率电平下工作，并且仅限于相对较低的频率。在高频下，构建具有足够大动态范围的模拟乘法器远非易事。

开关调制器的核心思想

或者，我们可以使用基于开关的电路来执行必要的乘法。这种调制器背后的关键思想是，将消息信号m（t）乘以具有基频fc的任何周期函数g（t），产生fc及其谐波的AM波。如果我们假设g（t）是一个具有基频fc的偶数周期函数，我们可以将其展开为以下形式的傅里叶级数：

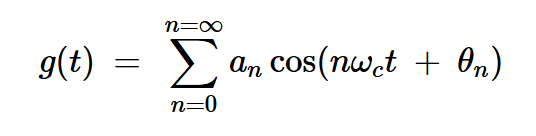
方程式3

将消息信号乘以g（t），我们得到：

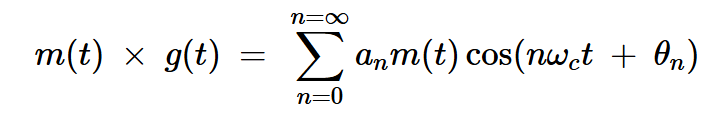
方程式4

方程4中的信号是以⍵c、2 9077》c、3 9077 c等为中心的AM波的叠加。该方程表明，我们可以通过将消息信号乘以具有基频fc的任何周期函数g（t）来产生AM波。因此，不必将m（t）乘以纯正弦波来产生AM波。相反，我们可以选择一个更合适的函数g（t），使电路实现更容易。

有趣的是，如果g（t）是一个在0和1之间交替的方波，它就充当了一个门控函数，周期性地打开和关闭输入。在这种情况下，我们可以将乘法简化为开关操作。图2显示了如何通过单个开关实现此门控功能。

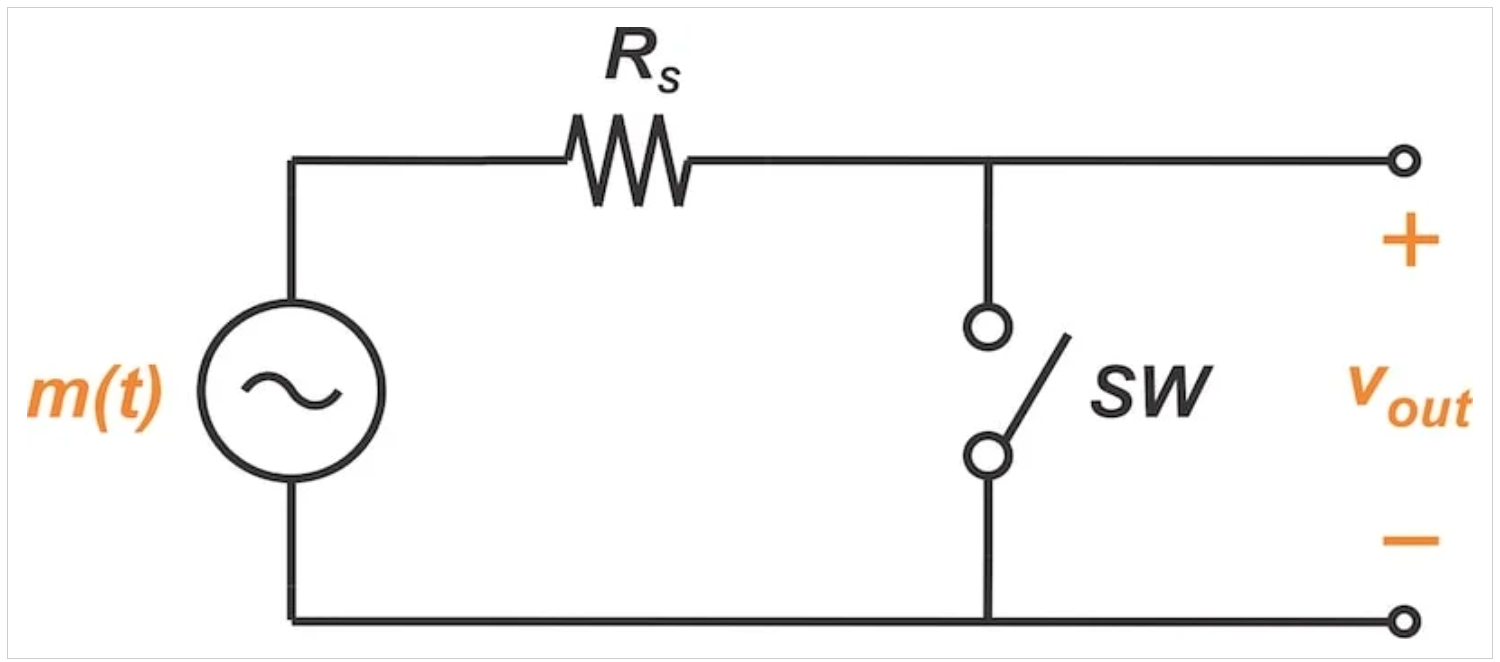
图2 单个开关可用于将输入乘以方波

在上述电路中，Rs模拟了源极电阻。当开关打开时，输入被传递到输出。当开关闭合时，输出降至零。因此，消息信号乘以在零和一之间切换的方波（图3）。

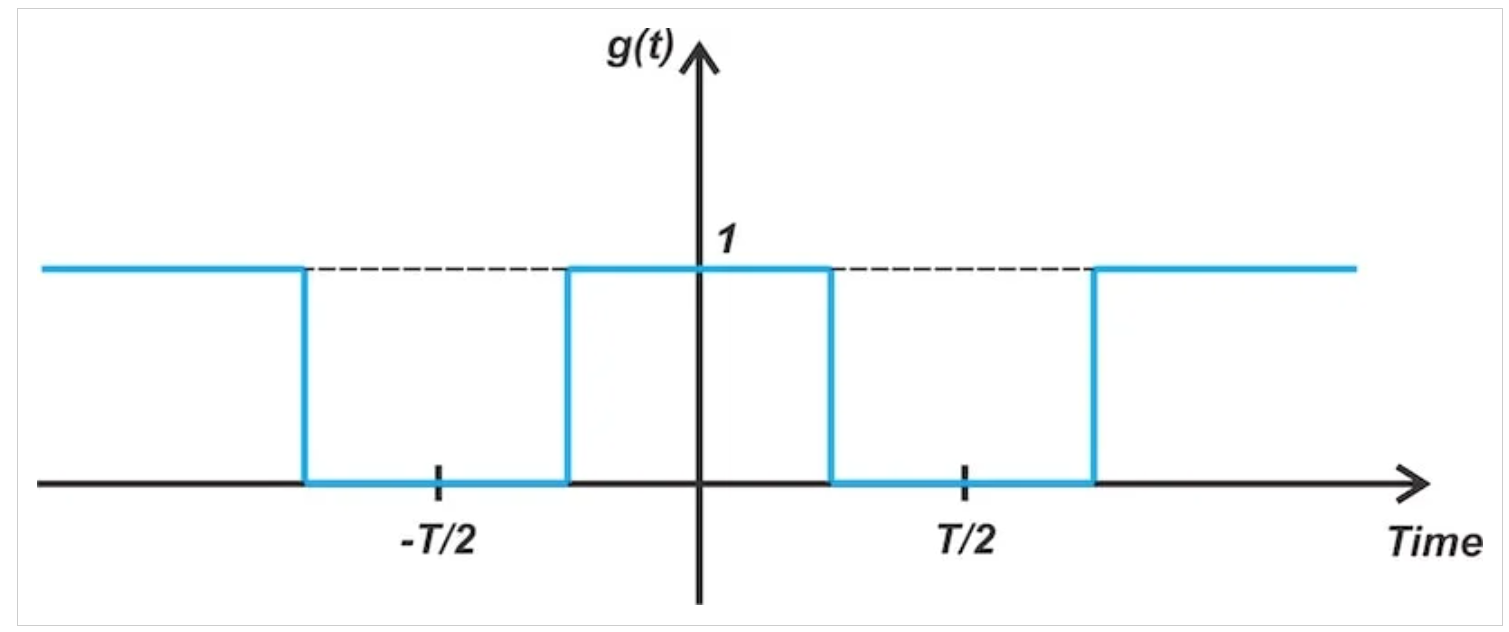
图3上述开关调制器中使用的门控功能

我们将在本文稍后更深入地讨论这一想法的实现。然而，在此之前，让我们检查一下电路的典型时域波形。

开关调制器的时域波形

为了检查时域行为，我们将单音正弦消息应用于电路。图4显示了消息信号（顶部）以及m（t）相乘的波形（底部）。

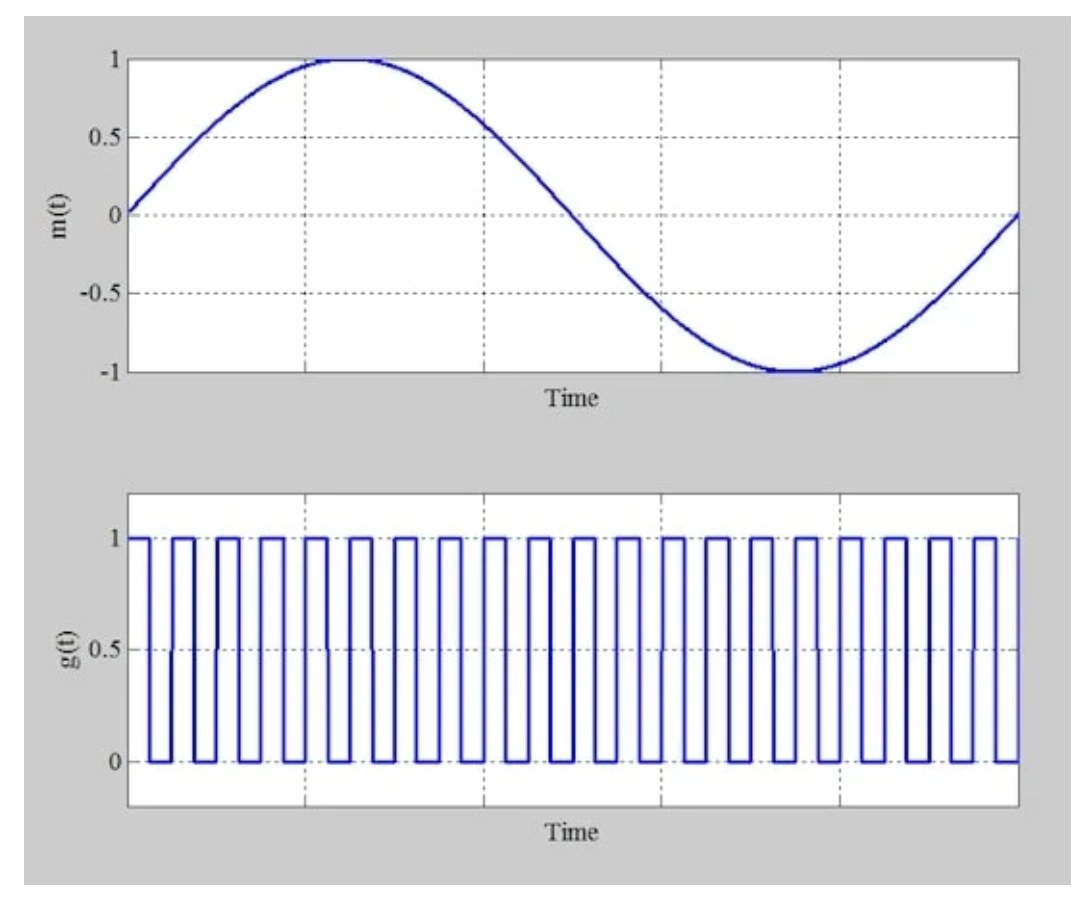
图4施加到调制器的单音输入（顶部）和有效倍增消息的波形（底部）

通过将这些波形相乘，我们得到了图5中的输出电压。

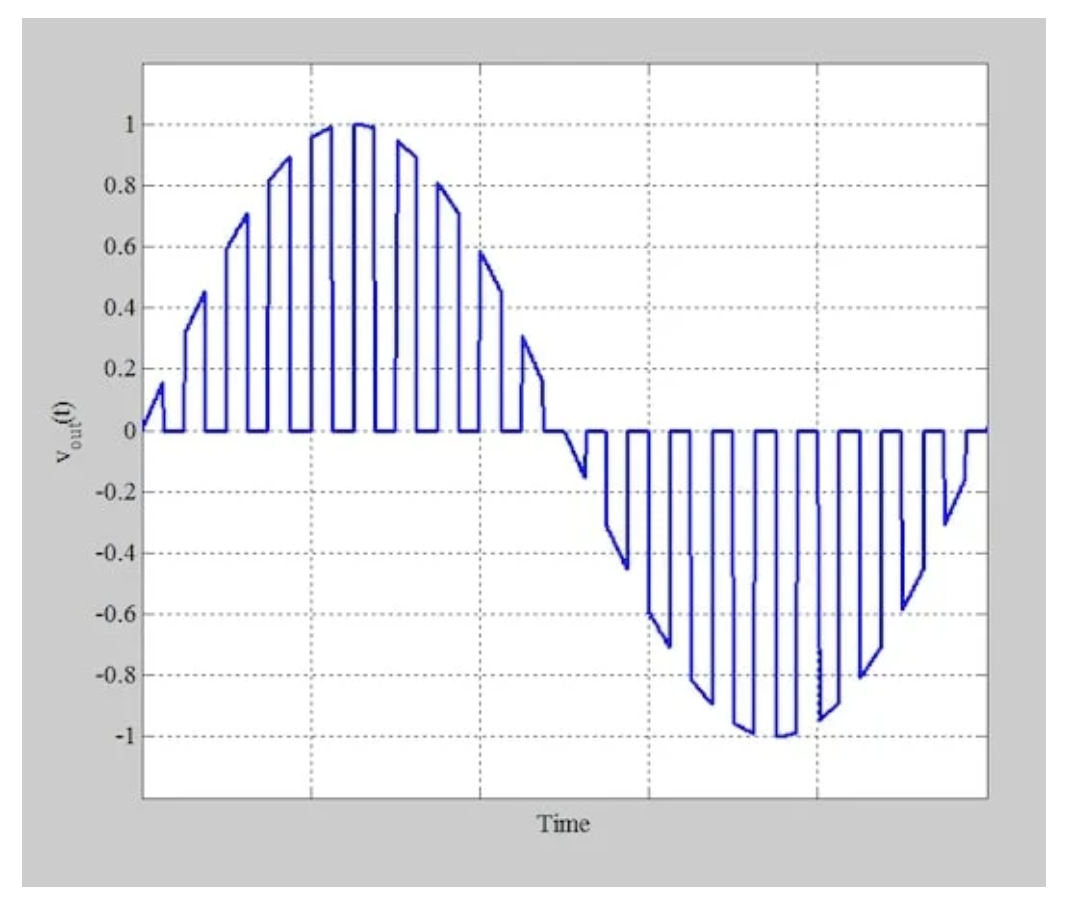
图5调制器产生的输出波形（vout）

正如预期的那样，输出电压在每个周期的一半与消息信号匹配，在另一半降至零。

虽然该波形的幅度类似于消息信号，但它不是典型的调幅信号。为了产生所需的AM信号，我们通过一个调谐到载波频率的带通滤波器。如图6所示。

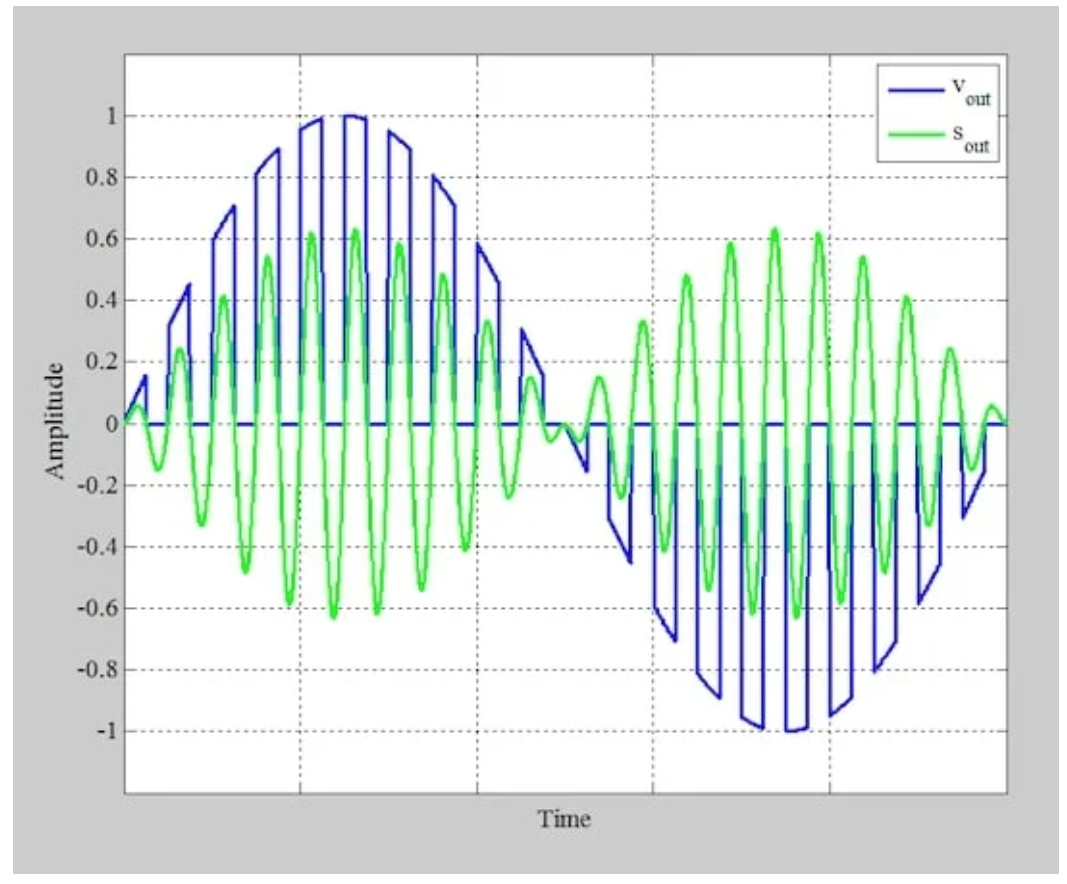
图6应用门控功能后的信号（蓝色）和带通滤波器输出端的结果信号（绿色）

我将在本文末尾提供一段代码摘录，以帮助您在MATLAB中执行必要的过滤。

电路实现：二极管桥式调制器

图7显示了如何使用二极管桥实现调制器的开关功能。

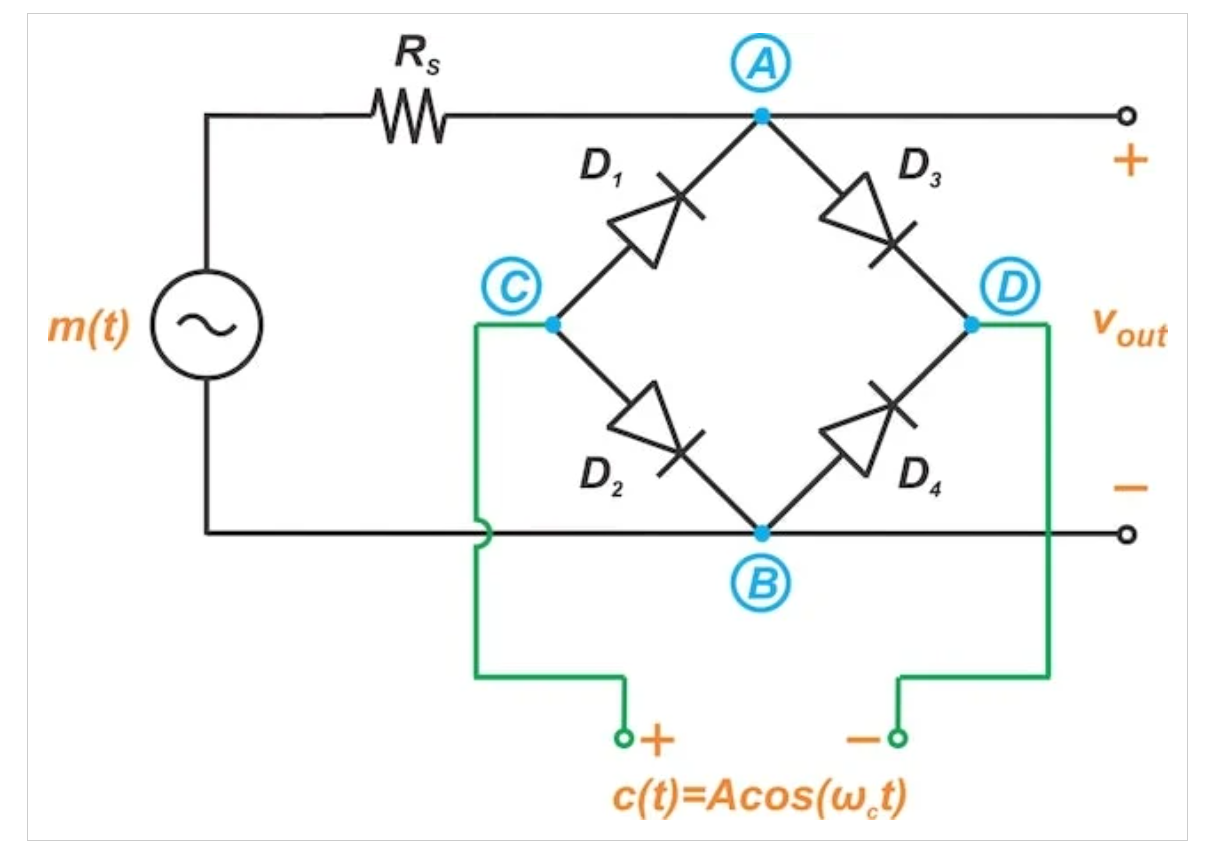
图7 二极管桥可用于构建开关调制器

当c（t）为大正值时，所有四个二极管都导通。当二极管D1和D2匹配，二极管D3和D4也匹配时，节点A和B处于相同的电势。因此，当c（t）为正值时，节点a和B有效地短路在一起。当c（t）为负时，所有四个二极管都开路，模拟节点A和B之间的开路开关。

最大开关频率取决于二极管的开启和关闭速度。

二极管桥调制器输出信号方程的推导

通过假设g（t）是一个在0和1之间切换的方波，我们可以使用傅里叶级数表示法将其扩展为余弦函数：

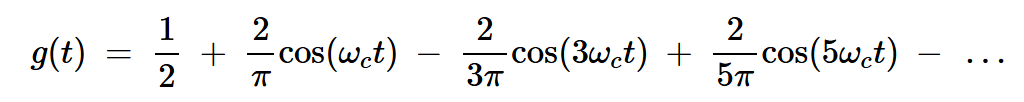
方程式5

因此，输出电压为：

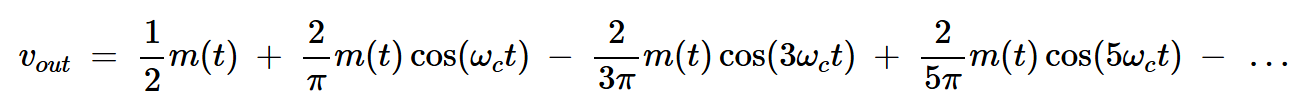
方程式6

输出频谱包括以0、±fc、±3fc、±5fc等为中心的消息频谱的副本。这如图8（b）所示。基带频谱的频谱见图8（a）。

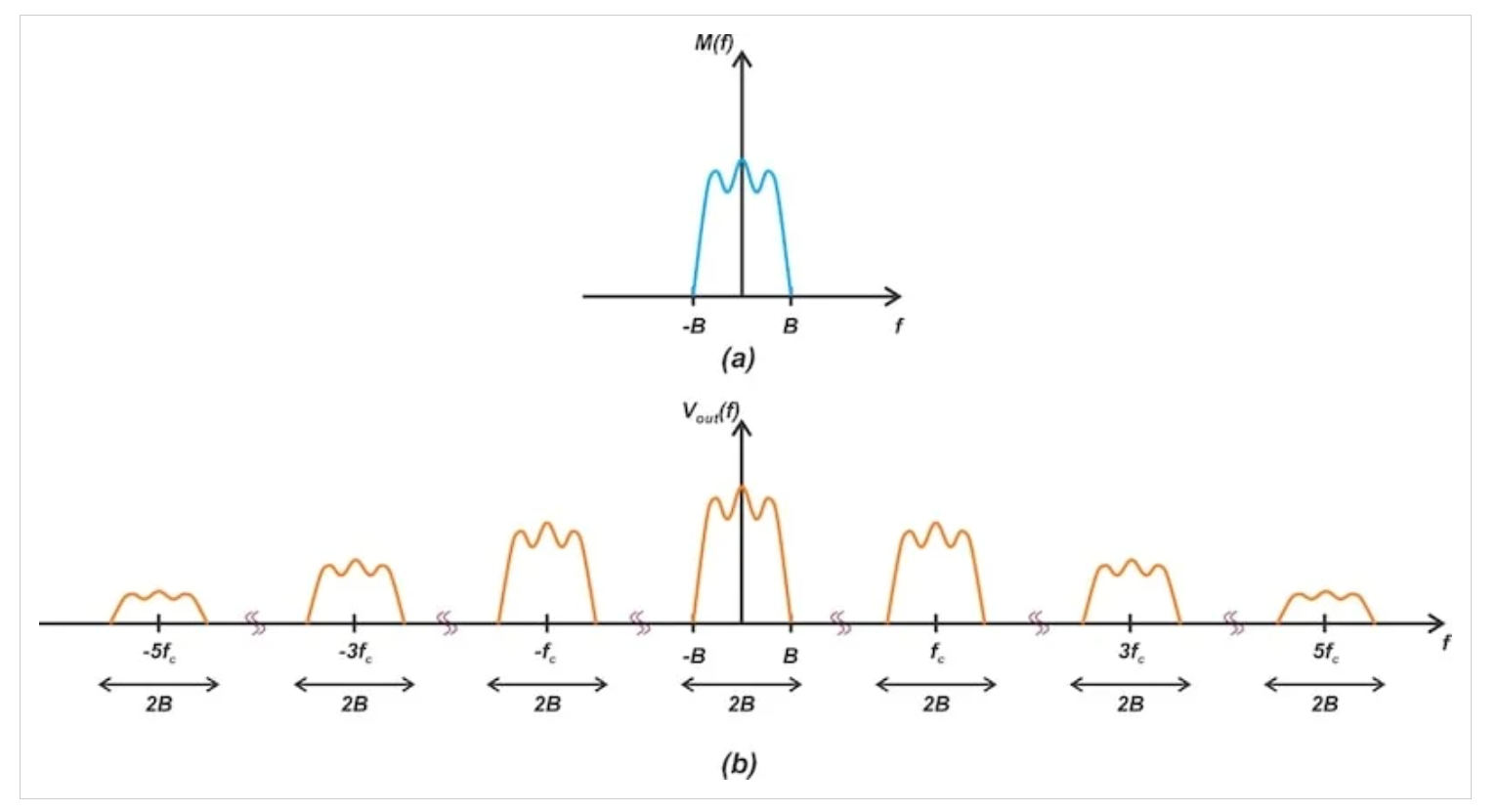
图8基带消息信号（a）和调制器（b）产生的信号的频谱

图8（b）中的输出频谱包括我们不想要的几个信号以及我们想要的信号。在得出最终的输出方程之前，我们需要滤除不需要的信号分量。

滤波以隔离AM信号

为了将以fc为中心的所需频谱与其他频谱分量分开，我们应该：

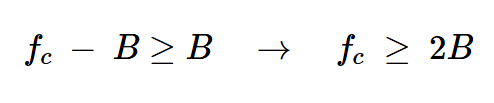
方程式7

其中B是基带信号的带宽。因此，我们需要将输出信号通过以fc为中心的带宽为2B的带通滤波器，以分离出所需的分量（图9）。

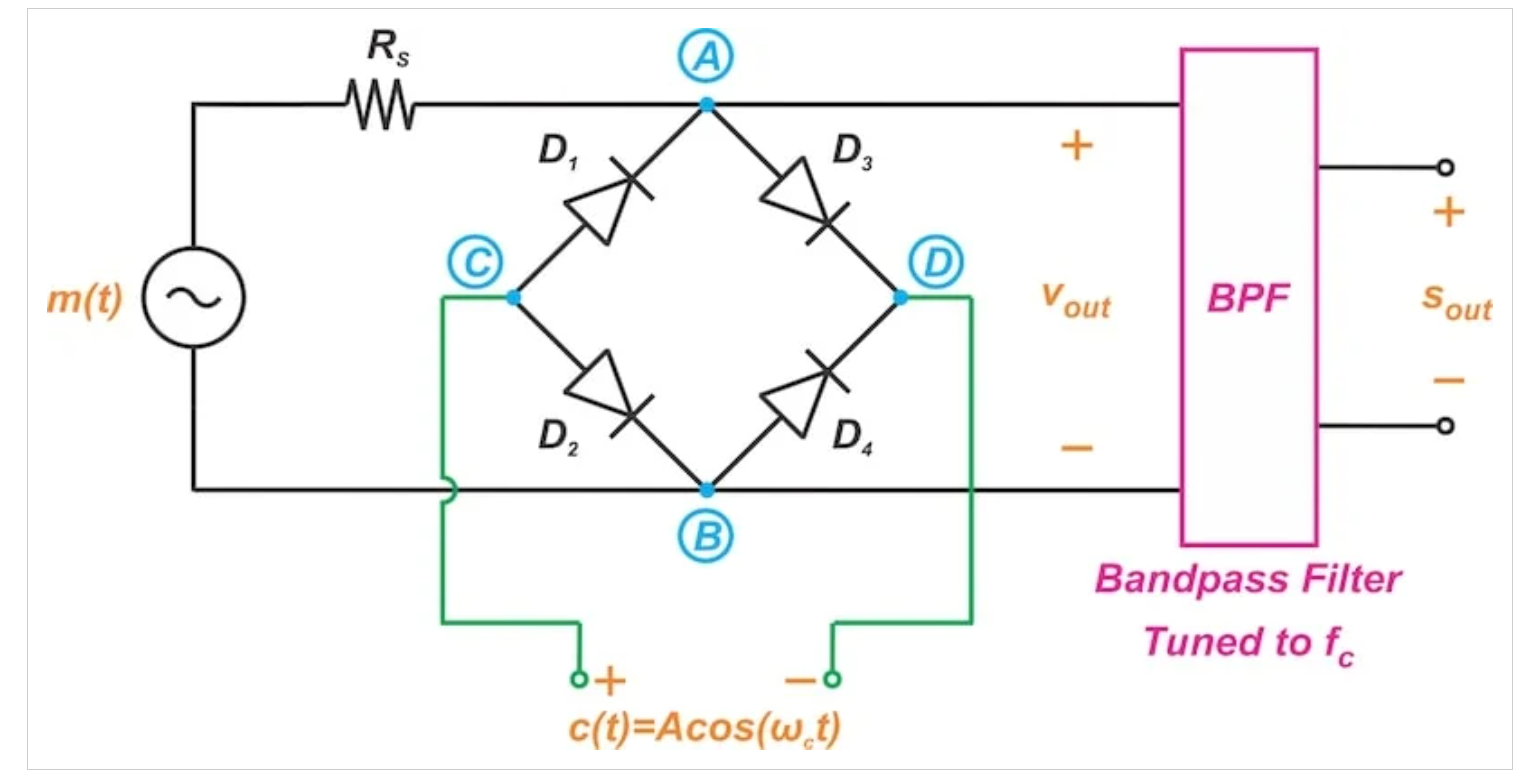
图9 带带通滤波器的二极管桥式调制器示意图

使用理想的带通滤波器，只有以fc为中心的频谱分量才能通过输出，导致：

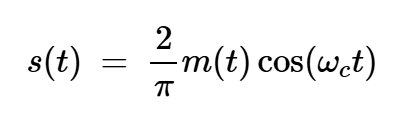
方程式8

让我们使用图6中所示的波形来验证这个方程。图中所示的调制信号是针对幅度为1的单音正弦消息获得的。对于|m（t）|≤1，方程8预测调制信号的最大值约为2/π≈0.64。这与图6中的绿色波形非常吻合，其最大值约为0.63。

在上述讨论中，我们使用了一个调谐到载波频率的滤波器来分离fc处的频谱分量。虽然我们可以将带通滤波器调谐到谐波频率，以产生更高频率的AM波，但我们通常更喜欢使用基频的分量，因为傅里叶系数随着我们向高次谐波移动而减小（见方程5）。

带通滤波器的MATLAB仿真

我使用MATLAB生成了图4至图6中的时域波形。如果你想重新创建这些波形并自己进行实验，我在这里包含了我用于过滤过程的代码。否则，对于初学者来说，创建带通滤波器可能有点棘手。

以下代码通过定义频率响应（H）并将其应用于频域中的AM信号，创建了一个具有锐边和单位增益的理想带通滤波器。您需要根据特定示例的参数调整截止频率（fc1，fc2）和采样频率（fs）。

总结

虽然我们可以使用模拟乘法器来生成AM信号，但构建具有大动态范围的模拟乘法器很棘手。在高频下尤其如此。开关调制器基于这样的想法，即将输入乘以任何周期函数都可以在周期函数的基频和谐波频率下产生AM波。

为了帮助我们理解开关调制器在实践中是如何工作的，本文介绍了二极管桥式调制器。在下一篇文章中，我们将讨论另一种开关调制器电路：环形调制器。