带有次级LC滤波器的电流模式降压转换器的建模与控制
简介
本文引用地址:https://www.eepw.com.cn/article/201811/394743.htm利用ADC、PLL和RF收发器的现代信号处理系统设计通常需要更低的功耗和更高的系统性能。为这些噪声敏感的设备选择合适的电源始终是系统设计人员的难点。这些设计总是需要在高效率和高性能之间做出取舍。
传统上,LDO稳压器通常被用于为那些噪声敏感的设备供电。LDO稳压器能够抑制系统电源中经常出现的低频噪声,并且为ADC、PLL或RF收发器提供干净的电源。但是LDO稳压器通常效率较低,尤其是在LDO稳压器必须将高于输出电压几伏的电源轨降压的那些系统中。在这种情况下,LDO稳压器通常可提供30%至50%的效率,而使用开关稳压器则可实现90%甚至更高的效率。
开关稳压器虽然比LDO稳压器效率更高,但它们的噪声太大,无法在不显著降低ADC或者PLL的性能的同时,直接为它们供电。开关稳压器的噪声源之一是输出纹波,它可能在ADC的输出频谱中表现为明显的信号音或杂散。为避免降低信噪比(SNR)和无杂散动态范围(SFDR),最大程度地减少开关稳压器的输出纹波和输出噪声非常重要。
为了同时保持高效率和高系统性能,通常需要在开关稳压器的输出端增加一个次级LC滤波器(L2和C2),以减少纹波和抑制噪声(如图1所示)。然而,二级LC输出滤波器也具有相应的缺点。理想情况下,功率级传输函数的建模为四阶系统,很不稳定。如果再考虑电流环路1的采样数据效应,则完整的控制至输出的传递函数为五阶系统。另一种替代解决方案是检测初级LC滤波器(L1和C1)点的输出电压来稳定系统。然而,当负载电流很大时,由于次级LC滤波器上的压降很大,应用这种方法会导致输出电压调节性能较差,这在某些应用中令人无法接受。
本文提出了一种新的混合反馈方法,能够在应用中采用带有次级LC滤波器的开关稳压器为ADC、PLL或RF收发器提供高效率、高性能的电源,同时在所有负载条件下提供足够的稳定性裕量并保持输出精度。
有些已经发表的关于带有次级LC输出滤波器的DC-DC转换器的研究性文章2-5,具体而言,《带有低电压/高电流输出的二级DC-DC转换器的控制环路设计》和《带有二级LC输出滤波器的高带宽交流电源的多环路控制方案的比较评估》这两篇文章讨论了二级电压模式转换器的建模和控制(该转换器不能直接应用于电流模式转换器)。文章《用于电流模式控制转换器的次级LC滤波器分析和设计技术》和《用于多模块转换器系统的三环路控制》讨论了带有次级LC滤波器的电流模式转换器的分析和建模。不过,这两篇文章都假设次级电感的电感值比初级电感小得多,这在实际应用中并不总是合适。
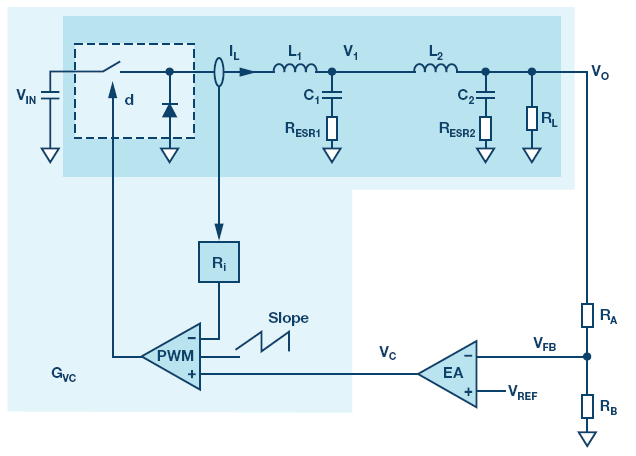
图1.带有次级LC滤波器的电流模式降压转换器的电路图。
本文分析了具有次级LC滤波器的降压转换器的小信号建模。提出了一个新的五阶控制至输出的传递函数,无论外围电感和电容参数如何,都非常精确。提出了一种新的混合反馈方法,可在提供足够的稳定性裕量的同时保持输出电压良好的直流精度。首次分析了反馈参数的限值,为实际设计提供了基本依据。基于功率级小信号模型和新的混合反馈方法,设计了补偿网络。利用奈奎斯特图评估了闭环传递函数的稳定性。提供了一个基于电源管理产品ADP5014的简单设计实例。借助次级LC滤波器,ADP5014在高频范围内的输出噪声性能甚至优于LDO稳压器。
附录I和附录II分别列出了功率级和反馈网络所需的小信号传递函数。
功率级小信号建模
图2显示了对应于图1的小信号框图。控制环路由内部电流环路和外部电压环路组成。电流环路中的采样数据系数He(s)是指Raymond B. Ridley在《用于电流模式控制的新型连续时间模型》中提出的模型。请注意,在图2所示的简化小信号框图中,假设输入电压干扰和负载电流干扰为零,因为本文不讨论与输入电压和负载电流相关的传递函数。
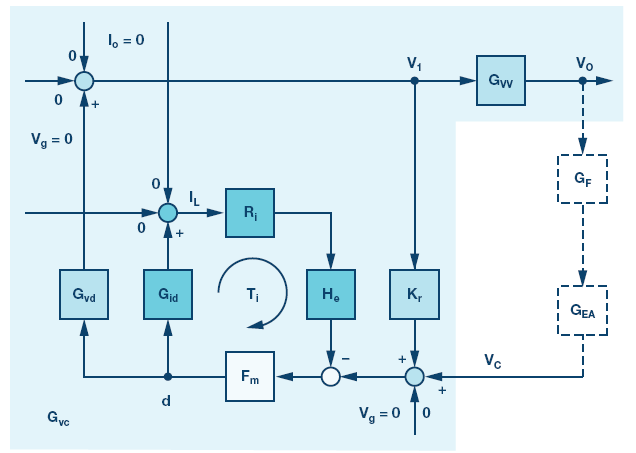
图2.带有次级LC滤波器的电流模式降压转换器的小信号框图。
降压转换器示例
使用电流模式降压转换器所演示的新的小信号模型具有以下参数:
► Vg = 5 V
► Vo = 2 V
► L1 = 0.8 μH
► L2 = 0.22 μH
► C1 = 47 μF
► C2 = 3× 47 μF
► RESR1 = 2 mΩ
► RESR2 = 2 mΩ
► RL = 1 Ω
► Ri = 0.1 Ω
► Ts = 0.833 μs
电流环路增益
我们关心的第一个传递函数是在占空比调制器的输出点测得的电流环路增益。由此产生的电流环路传递函数(见附录I中的公式16)表现为具有两对复数共轭极点的四阶系统,该系统产生两个系统谐振频率(ω1和ω2)。这两个谐振频率均由L1、L2、C1和C2决定。负载电阻RL以及C1和C2产生主零点。一对复数共轭零点(ω3)由L2、C1和C2决定。此外,电流环路中的采样数据系数He(s)将在开关频率的1/2处引入一对复数的右半平面(RHP)零点。
与不带次级LC滤波器的传统电流模式降压转换器相比,新的电流环路增益增加了一对复数共轭极点和一对复数共轭零点,并且它们彼此的位置非常接近。

图3.降压转换器电流环路增益。
图3显示了具有不同外部斜坡值的电流环路增益图。对于没有外部斜率补偿(Mc= 1)的情况,可以看出电流环路中的相位裕量非常小,这可能导致次谐波振荡。通过增加外部斜率补偿,增益和相位曲线的形状不会改变,但增益的幅度将减小,相位裕量将增加。












评论