小波的秘密1-小波变换概况与综述
1.有了Fourier,为什么还需要Wavelet?
本文引用地址:https://www.eepw.com.cn/article/201704/346253.htm先来揭揭短:
(1)Fourier分析不能刻画时间域上信号的局部特性。
(2)Fourier分析对突变和非平稳信号的效果不好,没有时频分析。
傅立叶变换将函数投影到正弦波上,将函数分解成了不同频率的正弦波,这不能不说是一个伟大的发现,但是在大量的应用中,傅立叶变换的局限性却日趋明显,事实上在光滑平稳信号的表示中,傅立叶基已经达到了近似最优表示,但是日常生活中的信号却并不是一直光滑的,而且奇异是平凡的,傅立叶在奇异点的表现就着实让人不爽,从方波的傅立叶逼近就可以看出来,用了大量不同频率的三角波去逼近其系数衰减程度相当缓慢,而且会产生Gibbs效应。其内在的原因是其基为全局性基,没有局部优化能力,以至局部一个小小的摆动也会影响全局的系数。实际应用中很需要时频局部化,傅立叶显然缺乏此能力了。即使如此,由于其鲜明的物理意义和快速计算,在很多场合仍然应用广泛。傅立叶变换在从连续到离散的情形是值得借鉴与学习的,大家都知道,时间周期对应频域离散,时间离散对应频域周期,时间离散周期对应频域离散周期,DFT其实是将离散信号做周期延拓然后做傅立叶变换再截取一个周期,反变换同样如此,所以DFT用的是块基的概念,这样如果信号两端的信号连接后不再光滑(即使两边都光滑),同样会在边界上产生大幅值系数(边界效应),延伸到图像中就是块效应。当对信号做对称周期延拓后再做傅立叶变换得到的正弦系数全部为0,也就是任何对称函数可以写成余弦的线性组合,同样按照离散的思路构造得到的是离散块余弦基,即DCT变换,虽然DCT可以通过对称后周期延拓再变换减少了边界效应(两边信号接上了,但不一定平滑),但也不能消除块效应,尤其是图像变换中人为将图像分成8*8处理后块效应更加明显。但是DCT很好的能量聚集效应让人惊奇,加之快速计算方法使它替代DFT成为图像的压缩的标准了很长时间(JPEG)。
闲扯了这么多,不要迷糊,开始上图:
第一个就是傅立叶变换是整个时域,所以没有局部特征。这是由基函数决定的,同时如果在时域发生突变,那么在频域就需要大量的正弦波去拟合,这也是傅立叶变换性质决定的。

第二个就是面对非平稳信号,傅立叶变换可以看到由哪些频率组成,但不知道各成分对应的时刻是什么。也就是没有时频分析,看不出来信号频域随着时间变换的情况,反过来说就是,一个的频图对应好几个时域图,不知道是哪个,这个在实际应用中就不方便了,如图:

如上图,最上边的是频率始终不变的平稳信号。而下边两个则是频率随着时间改变的非平稳信号,它们同样包含和最上信号相同频率的四个成分。做FFT后,我们发现这三个时域上有巨大差异的信号,频谱(幅值谱)却非常一致。尤其是下边两个非平稳信号,我们从频谱上无法区分它们,因为它们包含的四个频率的信号的成分确实是一样的,只是出现的先后顺序不同(时间分辨性太差)。
可见,傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
然而平稳信号大多是人为制造出来的,自然界的大量信号几乎都是非平稳的,所以在比如生物医学信号分析等领域的论文中,基本看不到单纯傅里叶变换这样naive的方法。

上图所示的是一个正常人的心电相关电位。对于这样的非平稳信号,只知道包含哪些频率成分是不够的,我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值——时频联合分析
2.预备知识:何为基?何为內积?
2.1 基
傅立叶变换和小波变换,都会听到分解和重构,其中这个就是根本,因为他们的变化都是将信号看成由若干个东西组成的,而且这些东西能够处理还原成比原来更好的信号。那怎么分解呢?那就需要一个分解的量,也就是常说的基,基的了解可以类比向量,向量空间的一个向量可以分解在x,y方向,同时在各个方向定义单位向量e1、e2,这样任意一个向量都可以表示为a=xe1+ye2,这个是二维空间的基:

而FT的基是不同频率的正弦曲线(整个时间),所以FT是把信号波分解成不同频率的正弦波的叠加和:而对于小波变换就是把一个信号分解成一系列的小波(短时间),也许就会问,小波变换的小波是什么啊,定义中就是告诉我们小波,因为这个小波实在是太多,一个是种类多,还有就是同一种小波还可以尺度变换,但是小波在整个时间范围的幅度平均值是0,具有有限的持续时间和突变的频率和振幅,可以是不规则,也可以是不对称,很明显正弦波就不是小波,什么的是呢,看下面几个图就是:

有了基,有什么用呢?下面看一个傅立叶变换的实例:
对于一个信号的表达式为x=sin(2*pi*t)+0.5*sin(2*pi*5*t); 下面看图形表示,感受一下频域变换给人的一目了然:

基具有非冗余性,即使基不是正交的,有相关性,但若去掉其中任何一个,则不成为基,这一点也叫完备性;基的表示有唯一性,即给定一族基对一个函数的表达是唯一的;一般情况下基非正交,也称为为exact frame(Resize basis),这个时候要表示信号可以将基正交化成唯一的正交基(对偶为其自身);也可以求其对偶框架(dual frame),其对应了小波变换中的双正交情形!信号可以依框架分解,然后用对偶框架重构。若在基集里添加一些新的向量,并随意调整空间位置,则有可能成为框架。把函数与基或框架作内积,也可以说成是一种函数空间到系数空间的变换。若某种变换后的能量(内积的平方和度量)仍然有一个大于0的上下界,才可以成为框架,由于框架的冗余性,所以系数的表达也不具有唯一性。若上下界相等,则为紧框架,且界表示冗余度。若上下界相等为且为1,称为pasval identity frame,此时不一定为正交基,此时若加上基的长度均为一的条件,则框架退化为正交基。可能你会问我们用基来表示信号就行了啊,为什么还要框架呢?其实很多信号表示方法不能构成基,却能构成框架,如短时傅立叶变换中如要求窗函数满足基条件,则可推出该函数有很差的时频局部化性质(事实上退化为了傅立叶变换)
2.2 內积
如果两个向量的内积为0 ,就说他们是正交的。
如果一个向量序列相互对偶正交,并且长度都为1,那么就说他们是正交归一化的。
3.小波诞生的前一个晚上:短时傅里叶变换(STFT)
有了缺点当然就想着改进了,这就出来了短时傅立叶变换,也叫加窗傅立叶变换,顾名思义,就是因为傅立叶变换的时域太长了,所以要弄短一点,这样就有了局部性。
定义:把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。下面就是示意图

时域上分成一段一段做FFT,不就知道频率成分随着时间的变化情况了吗!
可能理解这一点最好的方式是举例子。首先,因为我们的变换是对时间和频率的函数(不像傅立叶变换,仅仅是对频率的函数),它是二维的(如果加上幅度则是三维)。以下图所示的非平稳信号为例:

在这个信号中,在不同时刻有四个频率分量。0-250ms内信号的频率为100Hz,其余每个250ms的间隔的信号频率分别为50Hz,25Hz和10Hz。很明显,这是一个非平稳信号,让我们看一看它的短时傅立叶变换:用这样的方法,可以得到一个信号的时频图了:

既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四个频域成分,还能看到出现的时间。两排峰是对称的,只用看一排就行。这貌似解决了问题,好像有了加窗技术,整个世界都亮了。没有那么简单的,面对一个随机的非平稳信号,那么这个窗要多大了呢?(此时加窗傅里叶变换一脸的懵逼)
窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差。
窗太宽,时域上又不够精细,时间分辨率低。


下面通过一组实验,我们深入探索这种加窗技术,问题出现在哪里?



上图对同一个信号(4个频率成分)采用不同宽度的窗做STFT,结果如右图。用窄窗,时频图在时间轴上分辨率很高,几个峰基本成矩形,而用宽窗则变成了绵延的矮山。但是频率轴上,窄窗明显不如下边两个宽窗精确。所以窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需求。
4.小波来了
时势造英雄,小波开始一展拳脚了!
对于加窗傅立叶变换让人头疼的就是窗口的大小问题,如果我们让窗口的大小可以改变,不就完美了吗?答案是肯定的,小波就是基于这个思路,但是不同的是。STFT是给信号加窗,分段做FFT;而小波变换并没有采用窗的思想,更没有做傅里叶变换。小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间了~
就又回到了最开始的基了。
小波变换采用的这些基函数会伸缩、会平移(其实是两个正交基的分解)。缩得窄,对应高频;伸得宽,对应低频。然后这个基函数不断和信号做相乘。某一个尺度(宽窄)下乘出来的结果,就可以理解成信号所包含的当前尺度对应频率成分有多少。于是,基函数会在某些尺度下,与信号相乘得到一个很大的值,因为此时二者有一种重合关系。那么我们就知道信号包含该频率的成分的多少。如前文所述,小波做的改变就在于,将无限长的正弦函数基换成了有限长的会衰减的小波基。效果如下图:

从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函数的伸缩,平移量 τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。如下图

当伸缩、平移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。而当我们在每个尺度下都平移着和信号乘过一遍后,我们就知道信号在每个位置都包含哪些频率成分。看到了吗?有了小波,我们从此再也不害怕非稳定信号啦!从此可以做时频分析啦!
3.1解决了局部性

3.2解决时频分析



时域信号 FFT变换 小波分析
有了这些,小波分析也就入门了。
感谢大连理工大学机械工程硕士小木匠的出色工作。
感谢杜克大学方圆之中对STFT的现状所做的科普工作。



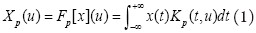
评论