- 1.有了Fourier,为什么还需要Wavelet? 先来揭揭短: (1)Fourier分析不能刻画时间域上信号的局部特性。 (2)Fourier分析对突变和非平稳信号的效果不好,没有时频分析。 傅立叶变换将函数投影到正弦波上,将函数分解成了不同频率的正弦波,这不能不说是一个伟大的发现,但是在大量的应用中,傅立叶变换的局限性却日趋明显,事实上在光滑平稳信号的表示中,傅立叶基已经达到了近似最优表示,但是日常生活中的信号却并不是一直光滑的,而且奇异是平凡的,傅立叶在奇异点的表现就着实让人不爽,从方
- 关键字:
小波 Fourier
- 上一小节中我们介绍了函数项级数的概念,这一节我们来讨论函数项级数的性质。傅立叶级数是一种函数项(三角函数)级数,本质上来说,一幅图像(或者一组信号)就是一个函数,我们研究图像的傅立叶变换,就是要探讨如何将图像函数用三角函数进行展开。所以如果要彻底搞清楚傅里叶变换,那么讨论函数项级数的性质是非常有必要的。在此基础上,我们将引入傅立叶级数的概念。 如果你对本文涉及的基础问题不甚了解,那么建议你阅读本文前面的部分。希望读者能日积月累,夯实基础。 完全搞懂傅里叶变换和小波(1)——总纲 http://w
- 关键字:
傅立叶级数 小波
- 1.4 傅立叶级数展开 之前我们在介绍泰勒展开式的时候提到过傅立叶级数。利用傅立叶级数对函数进行展开相比于泰勒展开式,会具有更好的整体逼近性,而且对函数的光滑性也不再有苛刻的要求。傅立叶级数是傅立叶变换的基础,傅立叶变换是数字信号处理(特别是图像处理)中非常重要的一种手段。遗憾的是,很多人读者并不能较为轻松地将傅立叶变换同高等数学中讲到的傅立叶级数联系起来。本节我们就来解开读者心中的疑惑。 如果你对本文涉及的基础问题不甚了解,那么建议你阅读本文前面的部分。希望读者能日积月累,夯实基础。
- 关键字:
傅里叶变换 小波
- 这一系列的文章中间中断了很久,很多朋友也留言希望我继续连载完,遂“重拾旧河山”,希望如果有时间能够把它做完。 本节我们介绍欧拉公式,它是复变函数中非常重要的一个定理,同时对于傅立叶变换的理解也必不可少。我们在高等数学里学习的傅立叶级数通常都是用三角函数形式表示的,而傅立叶变换中的一般都是用幂指数形式的,欧拉公式的作用正是把三角函数与e的幂指数联系到一起。 如果你对本文涉及的基础问题不甚了解,那么建议你阅读本文前面的部分。 完全搞懂傅里叶变换和小波(1)——总纲 http://www.eepw.
- 关键字:
傅里叶变换 小波
- 书接上文,之前我们介绍了高等数学里的三个中值定理,本节我们继续按照总纲的思路,用柯西中值定理来证明泰勒公式。这是我们循序渐进引出傅里叶的最后一项任务,完成这一步的学习之后,你就可以从级数的角度,了解傅里叶的意义了。 完全搞懂傅里叶变换和小波(1)——总纲 http://www.eepw.com.cn/article/201703/344766.htm 完全搞懂傅里叶变换和小波(2)——三个中值定理 http://www.eepw.com.cn/article/201702/344594.htm
- 关键字:
傅里叶变换 小波
- 书接上文,本文章是该系列的第二篇,按照总纲中给出的框架,本节介绍三个中值定理,包括它们的证明及几何意义。这三个中值定理是高等数学中非常基础的部分,如果读者对于高数的内容已经非常了解,大可跳过此部分。当然如果你需要对傅里叶变换有一个更深刻的认识,或者说从数学角度一点一滴完全搞懂它,为了体系的完整性,这部分知识还是必须的。 上篇文章链接地址:完全搞懂傅里叶变换和小波(1)——总纲 http://www.eepw.com.cn/article/201702/344594.htm 由于公式较多,这里只能
- 关键字:
傅里叶变换 小波
- 无论是学习信号处理,还是做图像、音视频处理方面的研究,你永远避不开的一个内容,就是傅里叶变换和小波。但是这两个东西其实并不容易弄懂,或者说其实是非常抽象和晦涩的! 完全搞懂傅里叶变换和小波,你至少需要知道哪些预备知识?主页君从今天开始就将通过一些列文章告诉你他们之间的来龙去脉!本节是全部系列文章的第一节——总纲,日后我们也将按照这个思路一点一点讲述所有的知识。需要说明的是,本文主要面向计算机专业或者电子信息专业的读者,为此我们将尽量采取一些非常非常基础的知识来帮助你理解。所以,题目里面讲的“完全搞懂
- 关键字:
傅里叶变换 小波
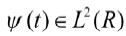
- 本文首先分析了基于小波变换图像压缩原理、流程和方法,然后针对传统的嵌入式小波零树压缩编码算法的不足,提出了改进方案。改进方案包括使用正交小波基Z97替代小波变换,使用排除法减少对重要系数的扫描次数,使用多种扫描顺序替换单一的“Z”字型扫描等。仿真实验结果表明,改进的方案提高了图像压缩效率,改善了重构图像的质量。
- 关键字:
小波 图像 压缩 算法 EZM 201607
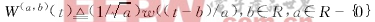
- 本文描述了基于正交小波函数族的多址通信原理,并提出了一种多速率正交小波调制方法.用具有不同伸缩尺度的小波函数对不同信道中的码流进行编码,可以达到扩展信息序列频谱的目的,因此这一多址技术具有很好的抗干扰性
- 关键字:
原理 及其 应用 通信 函数 正交 小波 基于
- 摘要:小波变换在电力系统谐波中的应用,与谐波本身的特性是直接相关的,要得到实时性和精确性都较高的检测效果就需要时电力系统的谐波特点,小波在这方面的应用原理有深刻的理解。文中对此在作了深入分析的基础上,
- 关键字:
检测 研究 谐波 电力系统 小波 变换 基于
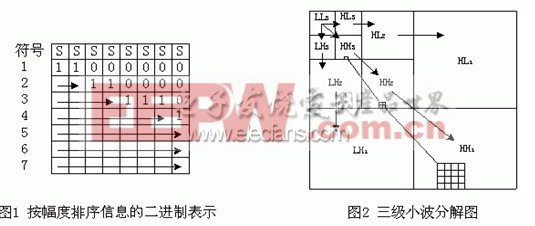
- 嵌入式零树小波EZW编码及其算法改进,在基于小波变换的图象压缩方案中,嵌入式零树小波 EZW(Embedded Zerotree Wavelets)[1]编码很好地利用小波系数的特性使得输出的码流具有嵌入特性。近年来,在对EZW改进的基础上,提出了许多新的性能更好的算法,如多级树
- 关键字:
算法 改进 及其 编码 小波 EZW 嵌入式

- DM642上5/3提升小波的优化,在新的图像压缩标准JPEG2000中,采用9/7、5/3提升小波变换作为编码算法,其中5/3小波变换是一种可逆的整数变换,可以实现无损或有损的图像压缩。在通用的DSP芯片上实现该算法具有很好的可扩展性、可升级性与易维护性
- 关键字:
优化 小波 提升 5/3 DM642
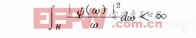
- 快速小波变换的定点DSP实现,小波变换具有良好的时——频局部性,是分析奇异信号的重要方法。定点DSP在工程中的应用十分普遍,具有低成本,高性能的特点。利用DSP实现小波变换可以满足工程是实时性的要求。文中简要介绍了小波变换理论
- 关键字:
DSP 实现 定点 变换 小波 快速
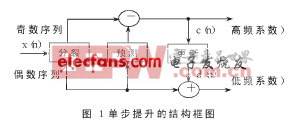
- 图像的二维提升小波变换的FPGA实现,小波分析理论以其良好的时频区域性和多分辨率分析能力,开辟了图像处理的崭新领域。小波变换是一种很好的图像分解方法,非常适合于分析突变信号而用于静止图像边缘的提取和压缩。高阶小波变化还可以用于实时处理视频
- 关键字:
FPGA 实现 变换 小波 二维 提升 图像
- 摘要:文中在应用对数域电路的基础上,提出了一种新型的连续小波变换方法,它通过对母小波的一种数值逼近得到小波函数的有理公式,并以Marr小波为例来模拟这个逼近过程,并用Matlab对逼近过程进行仿真。仿真结果显示
- 关键字:
变换 实现 小波 滤波器 SI 基于
小波介绍
您好,目前还没有人创建词条小波!
欢迎您创建该词条,阐述对小波的理解,并与今后在此搜索小波的朋友们分享。
创建词条
关于我们 -
广告服务 -
企业会员服务 -
网站地图 -
联系我们 -
征稿 -
友情链接 -
手机EEPW
Copyright ©2000-2015 ELECTRONIC ENGINEERING & PRODUCT WORLD. All rights reserved.
《电子产品世界》杂志社 版权所有 北京东晓国际技术信息咨询有限公司

京ICP备12027778号-2 北京市公安局备案:1101082052 京公网安备11010802012473