FPU加法器的设计与实现
摘要:浮点运算器的核心运算部件是浮点加法器,它是实现浮点指令各种运算的基础,其设计优化对于提高浮点运算的速度和精度相当关键。文章从浮点加法器算法和电路实现的角度给出设计方法,通过VHDL语言在OuartusII中进行设计和验证,此加法器通过状态机控制运算,有效地降低了功耗,提高了速度,改善了性能。
关键词:浮点运算;加法器;设计;VHDL;状态机
在一般的处理器中,浮点加法、减法、转换和传送最终都是可以转换为采用浮点加法器实现,所以浮点加法器的使用频率高达55%,是使用频率最高的浮点运算模块。浮点加法的两个特点,一是它复杂,二是它被使用的频率在所有操作里面是最高的,所以它是现代微处理器和数字信号处理器中非常关键的部分。因此.浮点加法器的设计对FPU的整体性能十分重要。
1 运算方法
最基本的浮点加法算法需要相对最多的串行运算操作,它需要完成两个浮点操作数的求和运算,包括尾数部分的求和以及相应修改结果的指数值,而且最终结果必须是符合正IEEE754标准的规格化浮点数。
根据IEEE754浮点数表示方法与运算规则,其表示如公式(1)所示:
![]()
公式中:s为尾数的符号;t为指数的符号;e为尾数;f为指数。存储格式如图1所示。

为方便浮点数的乘除法运算,文中将e=1.n的表示方法改为e=1n,这样不断减少了进行乘除运算后的额外移位操作而且不增加加减法运算的运算量。
一般情况下,在浮点运算中为了提高数据表示的精度,通常需要将一段离散数据在实数轴上集中表示,这就需要对浮点数的表示方法进行限制,因此在浮点数中尾数的位数应大于指数的值,这样表示的优点是其数据精度相对较高。
本浮点加法模块,将采用突破浮点数表示方法的上述限制,使指数的值可以远远大于尾数的位数,这样数据的表达范围增大,实数轴上较宽的一段离散数据就可表达。然而这种做法的缺点是,一方面当数据表示宽度增大后,其精度就会降低,原因是表示的汇聚点距离拉大;另外一种情况是会出现数据移空现象,例如当一个操作数很大,而另一个操作数很小时,如果要进行减法运算,会出现在对阶移位的过程中将一个操作数移成了空数据,其值将会变成零。因此当两个操作数进行加法运算时,假如它们之间的差距很大,就可以不进行运算,直接将较大的操作数直接输出作为运算结果,就可将无谓操作避免,从而节省运行时间。
对于浮点数加法运算来说,它要求参与运算的两个操作数有一个共同的特点,那就是指数相同。只有当两个操作数的指数相同时才能够进行加法运算。浮点数加法如公式(2)所示:
![]()
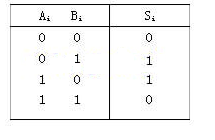
签于浮点加法运算的特殊要求,两个浮点操作数存进行运算时需要通过以下几个步骤完成。第1步进行0操作数的检查,如果判定两个操作数中任意一个操作数为零,则没有必要进行后续一系列的操作,直接输出结果,从而节省运算时间;第2步,看它们的阶码是否相同,也就是小数点是否对齐,若相同则表示对齐,否则就必须通过对阶使小数点对齐,即阶码相同。第3步,对阶结束后,进行尾数求和,方法和定点加法运算相同。第4步,对结果进行规格化。第5步,进行必要的舍入处理。另外在进行加法器设计时,将和减法一起进行考虑,采用补码运算,这样将来的操作就可以直接调用加法核去完成。






评论