SVM与Fourier算法在电网短期负荷预测中的应用

本文将Fourier(傅立叶)算法与SVM(支持向量机)共同引入电网短期负荷预测。对于波动性较大的负荷，Fourier算法用于滤除高次谐波分量。SVM用于对滤除了高次分量的数据进行统计学习，它首先筛选与预测点相关的的历史数据构成训练样本，再将预测的平滑性和误差损失函数相结合构成问题的目标函数进行求解。编制了相应的软件，对某实际电网进行了短期负荷预测，取得了理想的结果。
　　关键词：支持向量机，傅立叶，损失函数，短期负荷预测，核函数

Application of SVM
to power system short-term load forecast


Yang Jingfei, Cheng Haozhong


(Department of Electrical Engineering, Shanghai Jiaotong University,
Shanghai ,200030,China)

Abstract: This paper introduces Fourier algorithm and SVM algorithm to short-term load forecasting of power system. Fourier method is applied to get rid of the high frequency harmonics. The data without high frequency harmonics are then utilized by the statistics learning method of SVM(support vector machines). Sample data are constituted by filtering the historical data through clustering method. The object function takes both the fatness of prediction and error loss function into consideration. Corresponding software was developed and used to forecast the short-term load of a practical power system, and the final forecast error is low.
Key words: support vector machines, Fourier algorithm, loss function, short-term load forecasting, kernal function

0 引言
　　电力系统负荷预测是电网能量管理系统的重要内容，通过精确的负荷预测，可以经济合理地安排机组启停，减少旋转备用容量，合理安排检修计划，降低发电成本，提高经济效益。常用的方法有非线性回归、神经网络法、时间序列法、模糊理论等。非线性回归和时间序列法在电网情况正常、生产和气象变化不大的时候预测效果良好，但不能考虑一些影响负荷的要素，如休息日、气象等，当这些因素发生突变时预测精度受到影响。神经网络和模糊理论考虑到了影响负荷的一些不确定因素，但没有彻底解决网络结构设计的难题，且需要较长的训练时间。
　　SVM(支持向量机)是由Vapnik[1]最早提出的一种统计学习方法，近年来已经被成功地应用于语音识别、文字识别、时序数列预测等领域。研究显示，该统计学习方法具有学习速度快、全局最优和推广能力强的优点，其学习结果经常明显好于其它的模式识别和回归预测方法。本文将SVM理论应用于电力系统短期负荷预测，既考虑了影响负荷的诸因素，又建立了完善的数学模型。
　　SVM算法对与预测负荷曲线较平滑的系统，能够取得较理想的效果。但是，对于惯性较小、随机波动性较强的中小型电网，其效果相对较差。改进的方法是，先采用Fourier算法将历史负荷曲线分解为平滑曲线和随机波动曲线两部分，只采用平滑部分作为SVM的历史训练数据，能够取得更好的效果。

1 SVM线性回归模型
　　假设有一组训练数据，共有l个，其中第i个数据包含变量和与之相对应的变量xi∈Rn和与之相对应的变量yi∈R，SVM定义了一种机器(machine),用于确定x到y的映射关系x→f(X,a),a为可调参数，通过对已知数据的学习来确定它。在线性回归中，定义映射函数f(x)=w,x>+b,w∈Rn,y∈R,并要求：1)找到最小的w以保证曲线的平滑性，一种常用的方法是使得w的欧氏二范数最小。2)映射的误差在允许的ε范围之内。可以写成下列数学模型：

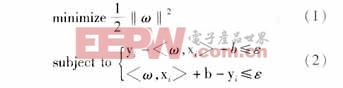
　　满足(2)式有时候会使问题的求解变得非常困难，可以通过在目标函数中增加损失函数来进行处理，损失函数有多种形式，本文中只考虑ε－intensive损失函数:

　　式中C为常数，是回归精度超过允许值的惩罚因子。(4)为有条件约束的优化问题，根据非线性规划对偶性理论，对其建立没有约束条件的Lagrange方程，并将最小值问题它转化为对偶的最大值问题：

2 非线性回归模型及其核函数
　　当然，现实中的大部分问题并不是简单的线性问题，对非线性问题进行回归，可以通过映射φ:X→τ把xi映射到特征空间τ，然后用核函数k(x,x′)=φ(x),φ(x′)>来代替线性回归中的x,x′>，根据文献[1]，支持向量回归的算法就可以改写为：

　　无论线性和非线性模型，都可采用内点法求解。