基于Taylor展开法整定MIC－PID控制器参数
加入技术交流群
2 MIC-PID控制器参数的整定
设一阶不稳定时滞过程为：
对式(20)分母中的纯滞后环节采用一阶Taylor逼近得
从式(22)可以看出纯滞后时间必须小于时间常数，即必须满足τ≤T，否则等效对象是不稳定的，由此可见，这一结果不适合大纯滞后对象。
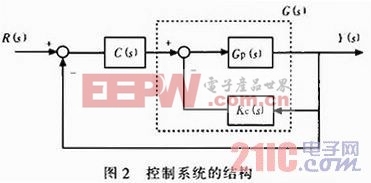
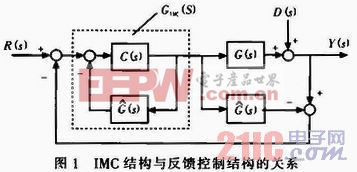
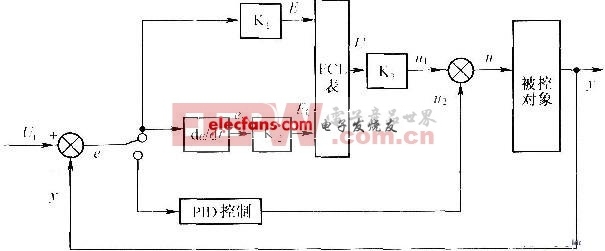
经过内环参数整定后，内环路可以用一个等效稳定对象G(s)来代替，如果外环路采用内模控制方法，则控制系统的等效框图仍如图1所示。
这里，αa一般取O．05至0．1之间的某个常数。
3 控制过程仿真
设被控过程对象模型为：
，这里取ε=2，按式(27)、(28)、(29)整定PID参数，得K=0．344 75，Ti=3.331，TD=0．399 9；当取ε=4时，得K=0．218 3，Ti=3．164 3，TD=0．263 1。当取ε=6时，得K=0．159 4．Ti=3．081，TD=0．195 9。取α=0．05，其响应曲线如图3所示。设被控过程对象模型为：
，这里取ε=1，按式(27)、(28)、(29)整定PID参数，得K=0．725 5Ti=1．982 2，TD=0．208；当取ε=2时，得K=0．463 4，Ti=1．898 9，TD=0．137 4其响应曲线如图4所示。 
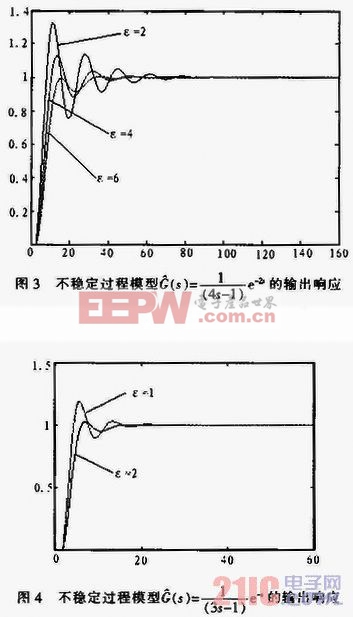
由图3和图4可见，如果纯滞后时间变小有利于系统稳定，纯滞后时间变大则系统容易发散，因此在整定参数时，可以人为地将延迟时间加大，以防止参数摄动时，系统不稳定。
4 结论
文中采用内模控制原理，针对一类不稳定时滞过程，采用双环控制结构，首先使广义对象(内环)稳定，然后按内模控制原理设计外环控制器，利用Taylor级数展开法得到了PID参数整定公式。通过仿真实例对IMC-PID控制器进行验证，结果表明在IMC-PID控制器的作用下被控系统不但具有良好的鲁棒性，而且调节快速，便于实际系统应用。
pid控制器相关文章:pid控制器原理
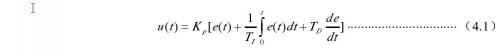
评论