基于SABER软件的数字控制电源系统的仿真设计

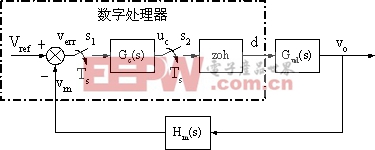
图2　控制系统框图

3.2 数字化控制算法的仿真设计

模拟部分的建模较为简单，只要根据已设计好的实际电路在仿真元件库中选取相应元件，并作必要的设置即可。对于数字控制部分，由于数据处理过程是离散化，为了充分模拟这一过程，可采用编程化的控制算法仿真设计。

首先对控制算法进行分析，因为它是控制电路的重要一环，也是构成闭环的关键。本例中控制算法采用PI算法，因为它简单可靠，在工程实践中有广泛的应用。如果采用其它的控制算法，也可以用下面的方法类似地得出相应的控制算法框图。

模拟系统中，PI控制算法的表达式为

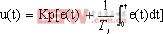（1）

式中u(t)为调节器的输出信号，即控制量；e(t)为基准与采样值的偏差信号；Kp为比例系数；T_I为积分时间常数。由于数字控制系统是一种采样控制系统，只能根据采样时刻的偏差计算控制量，因此，为使PI控制适用于数字控制系统，应将上述表达式离散化为

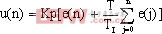（2）

该式称为PI调节的位置式PI控制算法^[4]。令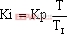(称为积分系数)，则可以得到离散化的位置式PI控制算法的编程表达式为

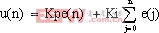（3）

令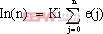，则表达式(3)可以改写为

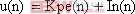（4）

当实际的数字控制系统出现开机或停机等大幅度变动时，系统输出会出现较大偏差，经积分累积后，该算式中的积分项容易出现积分饱和，导致控制效果变差，因此在积分项中加入抗饱和项，即

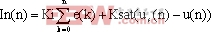（5）

其中，Ksat为抗饱和积分系数。^[5]当控制量偏高时，积分项在原来的基础上减去一定数值，该数值与控制量的计算值和上限之间的差值有关；相反，则加上一定数值，该数值与控制量的计算值与下限之间的差值有关，从而有效地抑制积分饱和。

考虑到表达式的可实现性，将积分项改为前一次的积分结果，从而得到下面的表达式

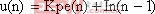（6）

由表达式(4)、(5)和(6)可以得出图3所示的PI计算框图。输入量为基准值与本次采样值之间的误差，输出量为带有抗饱和环节的PI计算输出。该框图将作为仿真电路控制部分建模的主要依据。

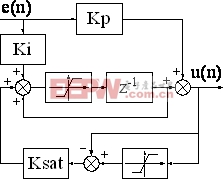
图3　PI计算框图