频率响应法-相对稳定性分析
 |
(2)由题意得![]() ,即
,即![]() 。在
。在![]() 处的对数幅值为
处的对数幅值为
上式简化后为
解之得,K=2.5。
根据![]() 的要求,则得
的要求,则得
即
利用三角函数的性质,可求得![]() 。于是有
。于是有
即
求解上式得![]() 。不难看出,K取2.5就能同时满足
。不难看出,K取2.5就能同时满足![]() 和
和![]() 的要求。
的要求。
5.5.3 对数幅频特性中频段与系统动态性能的关系
在分析控制系统的开环对数幅相频率特性时,习惯上将频率范围分为三个频段:低频段、中频段和高频段。其中低频段反映了控制系统的静态特性,关于此点在5.3.4中我们作了分析;中频段则反映了系统的动态特性,这是控制设计中一个非常关心的问题,这将在下面作介绍;高频段则主要反映了系统的抗干扰能力,对动态性能影响不大,将不作介绍。
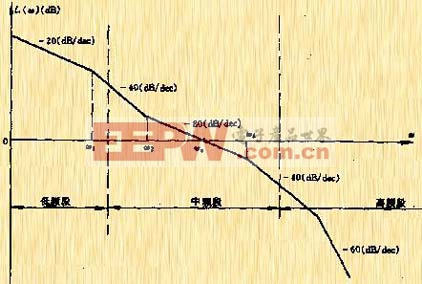 |
| 图5-56 对数幅频特性三个频段划分 |
中频段的主要参数有:剪切频率![]() 、相位裕量
、相位裕量![]() 和中频宽度h。对于图5-56所示系统,其中频宽度一般定义在斜率等于
和中频宽度h。对于图5-56所示系统,其中频宽度一般定义在斜率等于![]() 、靠近
、靠近![]() 处:
处:
|
一般要求最小相位系统的开环对数幅频特性在![]() 处的斜率等于
处的斜率等于![]() 。如果在该处的斜率等于或小于为
。如果在该处的斜率等于或小于为![]() ,则对应的系统可能不稳定,或者系统即使稳定,但因相位裕量较小,系统的稳定性也较差。下面通过二阶系统和三阶系统对上述结论进行说明。
,则对应的系统可能不稳定,或者系统即使稳定,但因相位裕量较小,系统的稳定性也较差。下面通过二阶系统和三阶系统对上述结论进行说明。
设一标准二阶系统的开环传递函数为:
|
式中,自然振荡频率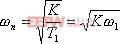 ,阻尼比
,阻尼比![]() ,其中
,其中![]() 为转角频率,则:
为转角频率,则:
(1) 当![]() 时,
时,![]() ,如图5-57a示,阶跃响应是衰减较慢的振荡过程;
,如图5-57a示,阶跃响应是衰减较慢的振荡过程;
(2) 当![]() 时,
时,![]() ,如图5-57b示,阶跃响应是衰减较快的振荡过程;
,如图5-57b示,阶跃响应是衰减较快的振荡过程;
(3) 当![]() 时,
时,![]() ,如图5-57c示,阶跃响应是接近无振荡的非周期过程;
,如图5-57c示,阶跃响应是接近无振荡的非周期过程;
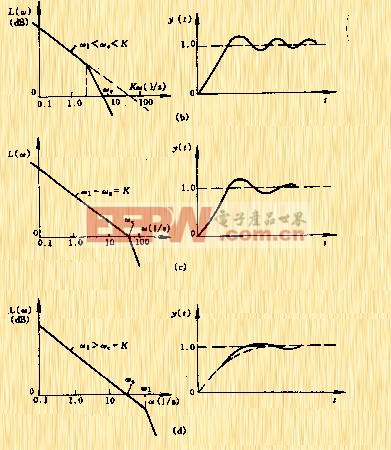 |
| 图5-57 二阶系统幅频特性和单位阶跃响应 |
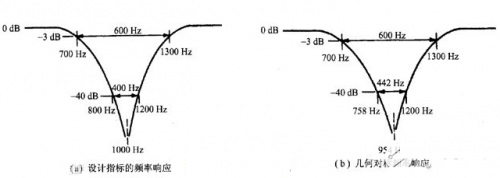
再设一个三阶系统的开环传函数为:
|
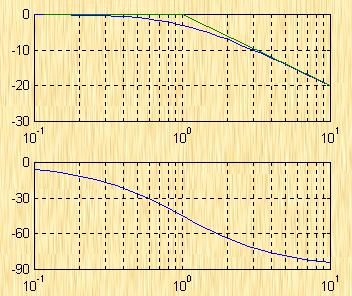
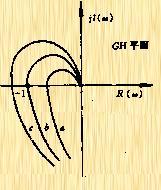
取K=0.1,1,10,100,得到如图5-58的幅频曲线a,b,c,d。由图可见。当![]() 时,式(5-59)的对数幅频特性曲线如图5-58所示的曲线
时,式(5-59)的对数幅频特性曲线如图5-58所示的曲线![]() 。剪切频率
。剪切频率 ![]()



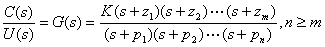

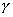
评论