频率响应法-相对稳定性分析
加入技术交流群
对应于图5－52的零分贝线上的点，即开环对数幅频特性曲线与
轴的交点；图5－50中相位穿越频率
的点在Bode图上是对应相角
的点，即相频曲线与 水平线的交点。从图5－50可见，相频特性曲线上对应于增益穿越频率
的点位于 水平线的上方。 |
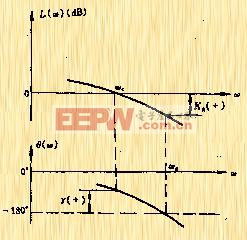| 图5－52 稳定系统的Bode图 |
 |
| 图5－53 不稳定系统的Bode图 |
在Bode图上，增益裕量常用分贝数表示，即
 |
|
上式表示系统在到达临界稳定前，允许系统增益增大的倍数。对于稳定的系统，由于
＜1，即
为负，由式（5－56）可知，增益裕量为正，这时对数幅频特性曲线上对应
的点在
轴下方，如图5－52；当系统不稳定时，相应地，可将图5－51绘制在Bode图上，如图5－53，这时相位裕量和幅值裕量均是负的。
增益裕量和相位裕量通常作为设计控制系统的频域性能指标。大的增益裕量和相位裕量表明控制系统是非常稳定的，但此时控制系统的响应速度将是非常慢的，而当增益裕量接近1或相位裕量接近零时，则对应一个高度振荡的系统。因此从工程的角度出发，一般控制系统设计时采用如下的裕量范围是比较合适的：
在
到
之间，增益裕量大于6dB。
同时需要指出，单独使用增益裕量或相位裕量作性能分析，都不足以说明系统的相对稳定性，必须同时给出这两个稳定裕量。对于大多数控制系统来说，这两个指标是统一的，但有时情况并非如此，图5－54a、图5－54b分别表示了这两种情况下的频率特性。
 |
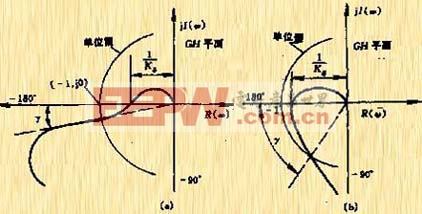| 图5－54 开环控制系统的奈氏图 (a) 好的幅值裕量和差的相角裕量 (b) 好的相角裕量和差的幅值裕量 |
例5－10 试求：（1）K＝1时系统的相位裕量和增益裕量。（2）要求通过增益K的调整，使系统的增益裕量
，相位裕量
。
例5－10 试求：（1）K＝1时系统的相位裕量和增益裕量。（2）要求通过增益K的调整，使系统的增益裕量 ，相位裕量 。
已知一单位反馈系统的开环传递函数为
 |
解 （1）基于在
处的开环频率特性的相角为
 |
即
 |
由三角函数的性质，有
 |
求得
。
同时，在 
处的开环对数幅值为
 |
 |
则
 |
根据K＝1时的开环系统传递函数，可知系统的
，从而
 |
 |
此小题也可用Matlab直接求解。
g=tf(1,conv([1,0],conv([0.2,1],[0.05,1])))
Transfer function:
1
-----------------------
0.01 s^3 + 0.25 s^2 + s
margin(g)
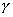
评论