频率响应法--极坐标图
控制系统中的时滞环节是典型的非最小相位系统。关于此点无论从它的近似展开式或其完整形式均可证明。同时从图5-30可以明显看出,最小相位系统的稳态误差为零,而非最小相位系统则是发散的。因此,对于控制系统而言,相位滞后越大,系统的稳定性越差,因此应尽可能减小或避免时滞环节对控制系统的影响。
5.3.4 系统开环对数幅频特性与闭环稳态误差的关系
对于一定的输入信号,控制系统的稳态误差与系统的类型和开环放大倍数有关。在给定了系统的开环幅频特性曲线后,即可根据其低频段的位置或斜率确定其稳态位置误差系数 ![]() 、速度误差系数
、速度误差系数 ![]() 和加速度误差系数
和加速度误差系数 ![]() 。对数幅频特性的低频段是由因式
。对数幅频特性的低频段是由因式 ![]() 来表征的,对于实际的控制系统,
来表征的,对于实际的控制系统, ![]() 通常为0span '>、1或2。下面分析系统的类型与对数幅频特性曲线低频渐近线斜率的对应关系及
通常为0span '>、1或2。下面分析系统的类型与对数幅频特性曲线低频渐近线斜率的对应关系及 ![]() 、
、 ![]() 和
和 ![]() 值的确定。
值的确定。
1.0型系统
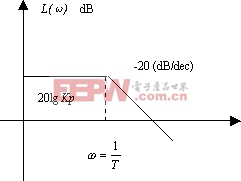 |
| 图5-31 0型系统的对数幅频特性 |
设0型系统的开环频率特性为
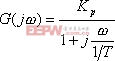 |
则其对数幅频特性的表达式为
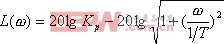 |
据此作出对数幅频特性曲线的渐近线如图5-31所示。由图可见,0型系统的对数幅频特性低频段具有如下特点:
1) 低频段的渐近线斜率为0 dB/dec,高度为![]() ;
;
2) 如果已知幅频特性低频段的高度,即可根据式:![]() 求出位置误差系数
求出位置误差系数 ![]() 的值,进而计算系统的稳态误差。
的值,进而计算系统的稳态误差。
2、I型系统
设I型系统的频率特性为
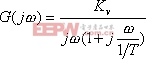 |
其对数幅频特性的表达式为
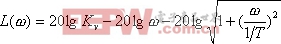 |
由上式作出的对数幅频特性曲线的渐近线如图5-32所示。
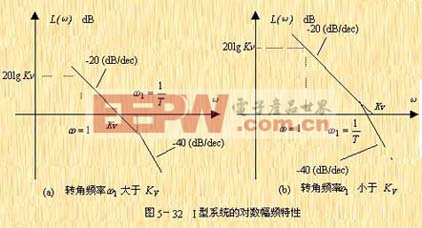 |
不难看出,I型系统的对数幅频特性有如下的特点:
1)低频渐近线的斜率为![]() 。
。
2)低频段渐近线(或其延长线)在 ![]() 处的纵坐标值为
处的纵坐标值为 ![]() ,由此可求出稳态速度误差系数
,由此可求出稳态速度误差系数 ![]() 。
。
3)开环增益即稳态速度误差系数![]() 在数值上也等于低频渐近线(或其延长线)与0dB线相交点的频率值。
在数值上也等于低频渐近线(或其延长线)与0dB线相交点的频率值。
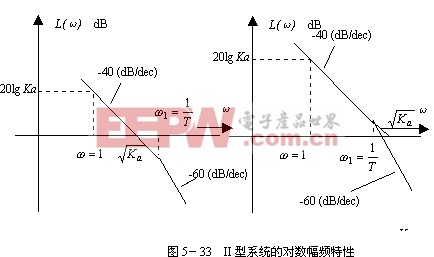
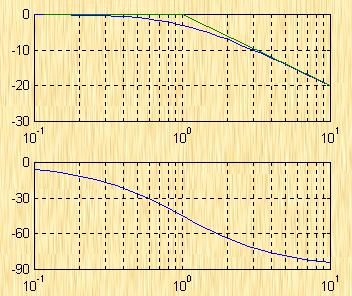
3、Ⅱ型系统
设Ⅱ型系统的频率特性
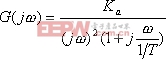 |
其对数幅频特性的表达式为
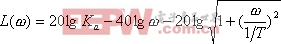 |
由上式作出对数幅频特性曲线的渐近线如图5-33所示。易知,Ⅱ型系统的对数幅频特性有如下的特点:
1) 低频渐近线的斜率为![]() 。
。
2)和I型系统一样,低频渐近线(或其延长线)在![]() 处的纵坐标值为
处的纵坐标值为 ![]() 由此可求出稳态加速度误差系数
由此可求出稳态加速度误差系数 ![]() 。
。
3) 系统的开环增益即加速度误差系数![]() 在数值上也等于低频段渐近线(或其延长线)与0dB线相交点的频率值和平方。
在数值上也等于低频段渐近线(或其延长线)与0dB线相交点的频率值和平方。
 |




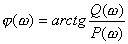
评论