频率响应法--极坐标图
加入技术交流群
随着 
的增大而单调地减小。这意味着，当 
时，幅值曲线不可能有峰值出现，即不会产生谐振。当 
时， 
有最小值，其值为期1
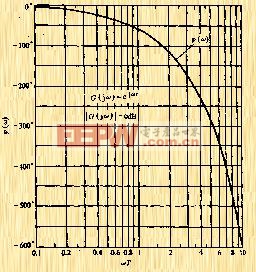
| 图5－27 时滞系统的相频特性 |
5.3.2 开环系统的伯德图
设系统的开环传递函数为
 |
则其对应的对数幅频和相频特性分别为
 |
因此，只要作出
所含各环节的对数幅频和相频特性曲线，然后对它们分别进行代数相加，就能求得开环系统的伯德图。
一般绘制开环系统伯德图的步骤如下：
（1）写出开环频率特性的表达式，将其写成典型环节相乘的形式。
（2）将所含各环节的转折频率由小到大依次标准在频率轴上。注意，由于比例环节和积分环节没有转折频率，因此可以排在最左边。
（3）绘制开环对数幅频曲线的渐近线。渐近线由若干条分段直线所组成，其低频段的斜率为
，其中 
为积分环节数。在 
处， 
。以低频段作为分段直线的起始段，从它开始，沿着频率增大的方向，每遇到一个转折频率就改变一次分段直线的斜率。如遇到 
环节的转折频率 
，当 
时，分段直线斜率的变化量为 
；如遇到 
环节的转折频率 
，当 
时，分段直线斜率的变化量为 
，其它环节用类似的方法处理。分段直线最后一段是开环对数幅频曲线的高频渐近线，其斜率为 
，其中n为 
的零点数。
（4）作出以分段直线表示的渐近线后，如果需要，再按照前述的各典型环节的误差曲线对相应的分段直线进行修正，就可得到实际的对数幅频特性曲线。
（5）作相频特性曲线。根据开环相频特性的表达式，在低频、中频及高频区域中各选择若干个频率进行计算，然后连成曲线。
例5-4试绘制开环系统的伯德图 ...
已知一反馈控制系统的开环传递函数为
 |
试绘制开环系统的伯德图。
解 系统的开环频率特性为
 |
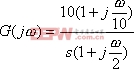由此可知，该系统是由比例、积分、微分和惯性环节所组成。它的对数幅频特性为
 |
按上述的步骤，作出该系统对数幅频特性曲线的渐近线，其特点为
1）由于
，因而渐近线低频段的斜率为 
。在 
处，其高度为 
。
2）当
时，由于惯性环节对信号幅值的衰减任用，使分段直线的斜率由 
变为 
。同理，当 
时，由于微分环节对信号幅值的提升任用，使分段直线的斜率上升 
，即由 
变为 
。
系统的相频特性按式：
进行计算。
上述作图过程同样可使用如下的Matlab语句绘制Bode图方法。
%ex5_4
function ex5_4
G=tf(10*[0.1,1],conv([1,0],[0.5,1]));%得到传递函数
[x0,y0,w]=bode(G);%由Bode函数获取幅值和相角
[x,y]=bode_asymp(G,w);%得到转折频率
subplot(211),semilogx(w,20*log10(x0(:)),x,y);%画幅频曲线和渐近线
subplot(212),semilogx(w,y0(:))%现相频曲线
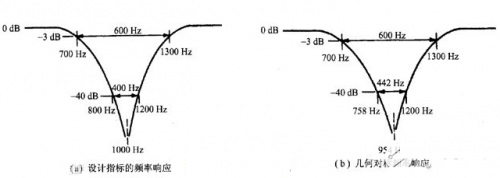
图5-28为该系统的伯德图。
的相位变化量为  ，系统b－29所示，相应的单位阶跃响应如图5－30。由图可见，最小相位系统的
相关推荐
技术专区 |
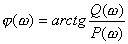
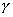
评论