频率响应法--极坐标图
|
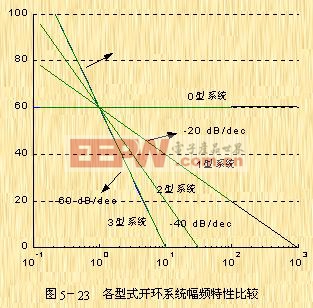 |
式(5-41)所示的是一簇斜率为![]() 的直线,且在
的直线,且在 ![]() 处,
处, ![]() ,如图5-23所示。由式(5-41)求得,这些不同斜率的直线通过0dB-44)中的1和
,如图5-23所示。由式(5-41)求得,这些不同斜率的直线通过0dB-44)中的1和 ![]() 项,则得
项,则得
![]()
上式表示![]() 的高频渐近线为一斜率
的高频渐近线为一斜率 ![]() 的直线。不难看出,两条渐近线相交于
的直线。不难看出,两条渐近线相交于 ![]() 。
。 ![]() 称为振荡环节的转折频率。基于实际的对数幅频特性既与频率
称为振荡环节的转折频率。基于实际的对数幅频特性既与频率 ![]() 和
和 ![]() 有关,又与阻尼比
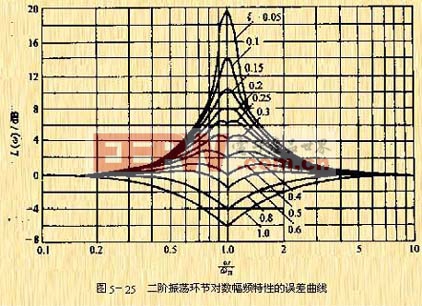
有关,又与阻尼比 ![]() 有关,因而这种环节的对数幅频特性曲线一般不能用其渐近线近似表示,不然会引起较大的误差。图5-25所示。由图可见,
有关,因而这种环节的对数幅频特性曲线一般不能用其渐近线近似表示,不然会引起较大的误差。图5-25所示。由图可见, ![]() 值越小,对数幅频曲线的峰值就越大,它与渐近线之间的误差也就越大。
值越小,对数幅频曲线的峰值就越大,它与渐近线之间的误差也就越大。
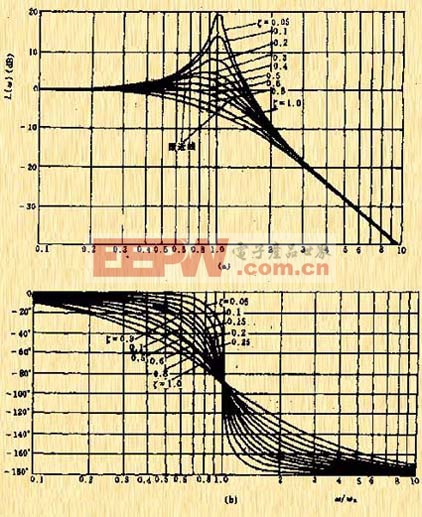 |
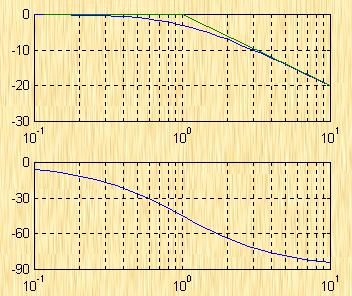
| 图5-24 二阶振荡环节的对数幅频特、渐近线和相角曲线 |
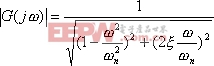
将式(5-43)的幅值表达式写为
 |
|
令
|
 |
显然,如在某一频率时,![]() 有最小值,则
有最小值,则 ![]() 便有最大值。把式(5-46)改写为
便有最大值。把式(5-46)改写为
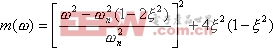 |
|
下面针对不同的![]() 值范围,讨论在什么条件下,式(5-44)会有峰值出现,这个峰值和相应的频率应如何计算。
值范围,讨论在什么条件下,式(5-44)会有峰值出现,这个峰值和相应的频率应如何计算。
(1)![]() 时
时
从式(5-47)中看出,当![]() 时,
时, ![]() 有最小值,即
有最小值,即 ![]() 有最大值,这个最大值称为谐振峰值,用
有最大值,这个最大值称为谐振峰值,用 ![]() 表示之。基于
表示之。基于 ![]() 值为
值为 ![]() ,由式(5-26所示。产生谐振峰值时的频率叫谐振频率,用
,由式(5-26所示。产生谐振峰值时的频率叫谐振频率,用 ![]() 表示,它的值为
表示,它的值为
由上式可见,当![]() 趋于零时,
趋于零时, ![]() 就趋向于
就趋向于 ![]() 。当
。当 ![]() 时,
时, ![]() 总小于有阻尼自然频率
总小于有阻尼自然频率 ![]() 。
。
(2)![]() 时
时
此时可将式(5-46)改写为
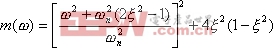 |
|
不难看出,由于![]() 随着
随着



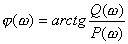

评论