控制系统的时域分析法--二阶系统的暂态响应
(2) 临界阻尼情况(ζ=1)
如果C(s)/R(s)的两个极点接近相等,则系统可近似看作临界阻尼系统。对于单位阶跃输入量,R(s)=1/s,因而C(s)可表示为
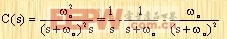 |
上式的拉普拉氏反变换为:
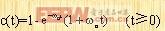 |
(3) 过阻尼情况(ζ>1)
这种情况下,C(s)/R(s)的两个极点是两个不等的负实数。对于单位阶跃输入量,R(s)=1/s,因此C(s)可以写成
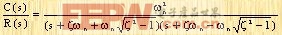 |
其拉普拉斯反变换为
 |
式中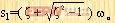 ,而
,而 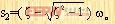 ,显然,这时系统的响应c(t)包含着两个衰减的指数项。
,显然,这时系统的响应c(t)包含着两个衰减的指数项。
当ζ远大于1时,在两个衰减的指数项中,一个比另一个衰减的要快得多,因此衰减得比较快的指数项(相应于较小时间常数的指数项),就可以忽略不计。也就是说,如果-s2与j 轴的距离比-s1要近得多(即|s1|>>|s2| ),那么在近似解中,可以忽略-s1,因为方程中包含s1的项比包含s2的项衰减得快的多,所以-s1对系统响应的影响,比-s2对系统的影响要小得多,因此忽略-s1是合理的。因此可以将C(s)/R(s)近似地表示为
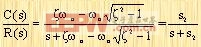 |
这一近似函数形式是根据下述条件直接得到的,即原来的函数C(s)/R(s)与近似函数的初始值和最终值,两者是完全相同的。
对于近似传递函数C(s)/R(s),其单位阶跃响应可表示为
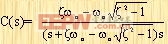 |
其时间响应c(t)为
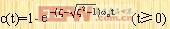 |
在过阻尼情况下,二阶系统的单位阶跃响应是随时间推移而单调增长,最后在t→∞时趋于稳态值,所以最大超调量是零,调整时间可以用近似的单位阶跃响应估算,如借用一阶系统单位阶跃响应的性质,可以认为响应达到稳态值的95%所需的调整时间
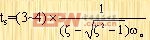 |
工程上,如果ζ》1.5时,使用上述近似式已有足够的准确度了。
3.5.2 二阶系统的暂态响应指标
当系统为欠阻尼情况下,即0 ζ1时,二阶系统阶跃响应的上升时间tr、峰值时间tp、最大超调量Mp的计算公式按式(3-13)可表示如下。
上升时间tr 令c(t)=1,代入式(3-13)中,即可求得tr。这时有
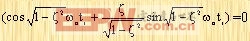 |
或
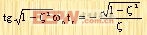 |
所以
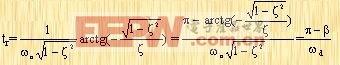 | (3-14) |
由上式可见,如欲减小tr,当ζ一定时,需增大ωn ,反之,若ωn一定时,则需减小ζ。
峰值时间tp 出现第一个峰时,单位阶跃响应随时间的变化率为零。为求tp,可将式(3-13)对时间t求导,并令其为零。于是得
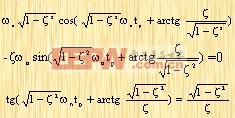 |
由此可知:
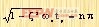 | n=0、1、2、…… |
到达第一个峰值时应有
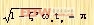 |
故得
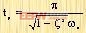 | (3-15) |
最大超调量Mp 最大超调量发生在t=tp,因此,令式(3-13)中的t=tp,并将tp值代入,即得以百分比表示的超调量
 | (3-16) |
调整时间ts 对于欠阻尼二阶系统,暂态响应可由式(3-13)求得为
 |
曲线 ,是系统对单位阶跃输入信号的暂态响应曲线的包络线,响应曲线c(t)总是包含在一对包络线之内,如图3-9所示。包络线的时间常数为1/(ζωn)。这样,当采用5%允许误差时,有
,是系统对单位阶跃输入信号的暂态响应曲线的包络线,响应曲线c(t)总是包含在一对包络线之内,如图3-9所示。包络线的时间常数为1/(ζωn)。这样,当采用5%允许误差时,有
| 1+ |
由上式得
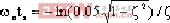 |
当0 ζ 0.8时,则有
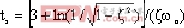 |
当采用2%允许误差时,则可推导得出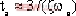
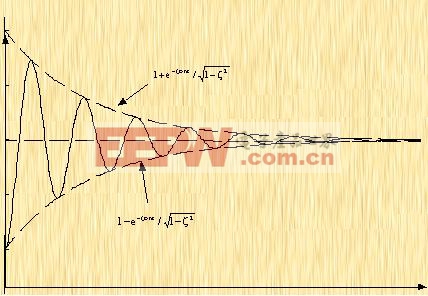 |
图3-9 二阶系统单位阶跃时间响应的包络线 |
3.5.3二阶系统的脉冲响应
当输入信号r(t)为单位脉冲函数时,相应的拉普拉斯变换为1,即R(s)=1。则二阶系统的单位脉冲响应C(s)为
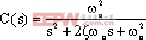 |
这个方程的拉普拉斯反变换,就是时域响应解c(t),这时当0≤ζ1时,
c(t)= (t≥0) (t≥0) |
当ζ=1时









评论