控制系统的时域分析法--控制系统的稳态误差

务请注意，使用拉普拉斯变换终值定理计算稳态误差终值的条件是：sEr(s)在s平面右半部及虚轴上除了坐标原点是孤立奇点外必需解析，亦即sEr(s)的全部极点除坐标原点外应全部分布在s平面的左半部。例如给定输入为正弦函数时

其象函数

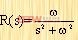在s平面的全部虚轴上不解析，就不能使用终值定理去求取系统的稳态误差终值。

3.2.4 动态误差

静态误差系数的一个明显特点，是对于一个给定系统只有一个系数呈现有限值，其它的系数不是零就是无穷大。因而，通过静态误差系数求得的静态误差或是零，或是有限的非零值，或是无穷大。所以，误差随时间的变化规律不能运用这种系数求出。但有些时候人们关心的往往是误差随时间变化的情况，这种误差表现了误差随时间变化的规律，称之为动态误差。本节介绍的动态误差将提供一些关于误差怎样随时间变化的信息，即，系统在给定的输入作用下稳态误差是否会与t，t2等成比例地增加。

动态误差不同但稳态误差系数相同的系统 首先论证两个具有不同动态误差的系统却能够有相同的静态误差系数。设以下的两个系统：

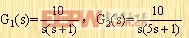其静态误差系数由下列各式给出:
Kp1=∞， Kp2=∞
Kv1=10， Kv2=10
Ka1=0， Ka2=0

于是，对于同样的阶跃输入，两个系统有相同的稳态误差。当然，对于斜坡和抛物线输入的稳态误差，该结论也同样适用。这个分析表明，不能根据静态误差系数去估算系统的动态误差。

动态误差系数 现在引进动态误差系数来描述动态误差。通过用E(s)/R(s)的分母多项式除它的分子多项式的方法，把E(s)/R(s)展开成下列s的升幂级数：

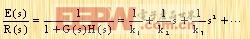幂级数的系数K1、K2、K3、…被定义为动态误差系数。对N型系统的动态误差系数由下式给出：

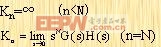其中
K1=动态位置误差系数；
K2=动态速度误差系数；
K3=动态加速度误差系数。

需要说明的是，在一个给定系统中，动态误差系数是与静态误差系数有关的。例如：设下列具有单位反馈的0型系统：

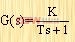其静态位置误差系数、静态速度误差系数和静态加速度误差系数分别是

其中
Kp=K
Kv=0
Ka=0

由于E(s)/R(s)可展开成

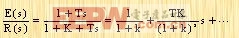所以，依据静态误差系数给出的动态误差系数如下：
k1=1+K=1+Kp

动态速度误差系数由下式给出：

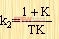当E(s)写成下面的形式时：
E(s)= R(s)+ sR(s)+ s2R(s)+…

动态误差系数的优点就更为清楚。这个级数的收敛域是s=0的邻域，这相当于在时域内的t=∞。假定所有的初始条件为零，并且忽略掉在t=0的邻域，这相当于在时域内的t=∞。假定所有的初始条件为零，并且忽略掉在t=0时的脉冲，则对应的时间解（即稳态误差）由下式求出：

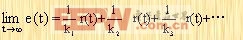这样，由输入函数和它的导数所引起的稳态误差能根据动态误差系数求出，这便是动态误差系数的一个优点。

如果E(s)/R(s)围绕原点展开成一个幂级数，级数的逐项系数就表示系统在缓慢变化的输入作用下的动态误差。动态误差系数是计算任意输入作用下的误差信号和稳态误差的简便方法。用这个方法就不需要实际去解系统的微分方程。

例3-9

设前向传递函数为G(s)= 的单位反馈控制系统，求出它的动态误差系数。还要求出当输入量为r(t)=a0+a1t+a2t2时的稳态误差。

对于该系统 = =0.1s+0.09s2-0.019s3+…

即 =0.1 (t)+0.09 (t)-0.019 (t)+…

则动态误差系数是 k1=∞

k2=1/0.1=10

k3=1/0.09=11.1

由于r(t)由下式给出：r(t)=a0+a1t+a2t²

得(t)=a1+a2t，(t)=2a2，(t)=0

于是，稳态误差为

= [0.1(a1+a2t)+0.09(2a2)]= (0.1a1+0.18a2+0.2a2t)

只要不是a2=0，稳态误差就变为无穷大。

由以上分析可知，如果E(s)/R(s)围绕原点展开成一个幂级数，级数的逐项系数就表示系统在缓慢变化的输入作用下的动态误差。动态误差系数是计算任意输入作用下的误差信号和稳态误差的简便方法。用这个方法就不需要实际去解系统的微分方程。