多传感器模糊—概率交互作用的数据关联算法
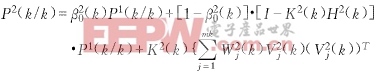
-V2(k)(V2(k))T}(K2(k))T (33)
令 ![]() (k/k)=
(k/k)=![]() 2(k/k),P(k/k)=P2(k/k)
2(k/k),P(k/k)=P2(k/k)
三、对加权系数Wj(k)的分析
为简化起见,省去式(12)中的i标注.式中的μA(Zj(k))表示第j个量测与目标航迹间的模糊关联度.P(Zj(k)/Zk-1)表示第j个量测与目标航迹之间的关联概率.P(A)为归一化系数.可见,加权系数Wj(k)实际上由模糊关联度和关联概率共同组成.
令 μj(k)=μA(Zj(k));βj(k)=P(Zj(k)/Zk-1).
则 Wj(k)=μj(k).βj(k)/P(A) (34)
μj(k)的求法在下一节给出;βj(k)的求法已在文献[3]中给出.
![]() (35)
(35)![]() (36)
(36)
其中ei(k)=exp{-(Vi(k))TS-1(k)Vi(k)};
b(k)=λ|2πS(k)|1/2(1-PDPG)/PD.
PG为正确测量落入跟踪门的概率,PD为正确测量的检测概率,λ为杂波密度.为简化起见,本文假设PD=PG=1.
进一步研究发现,在目标的匀速和匀加速运动段,PDAF可以较好地解决数据关联问题.当目标发生强机动时,由于密集杂波干扰,真实目标回波的新息Vj(k)增大,关联概率βj(k)减小.这将进一步使新息Vj(k)增大,关联概率βj(k)减小,最终导致关联失败,目标丢失,如图1所示.因此,当目标发生强机动时,单用PDAF方法将容易丢失目标.而在这种情况下,基于目标的机动特征,模糊逻辑关联方法却可以较好地解决目标的数据关联问题.所以,在目标不同的运动段,模糊关联度μj(k)和关联概率βj(k)应有不同的侧重,两者交互作用,充分发挥各自的优势,使系统的关联性能达到最佳.
模糊关联度μj(k)和关联概率βj(k)相互切换的依据是判定目标的运动状况.本文采用如下方法[4]检测目标的运动状况;首先,计算各时刻的所有有效回波新息之和![]() (k).其次,取一个长度为L的滑窗,滑窗内新息序列
(k).其次,取一个长度为L的滑窗,滑窗内新息序列![]() (k)的总和定义为:
(k)的总和定义为:
![]() (37)
(37)
根据统计量DL(k),用公式表示假设检验问题.在H0假设下,无机动目标时,DL(k)呈正态分布,其均值趋于零,方差为:
![]() (38)
(38)
式中s(i|i-1)为![]() (i)的方差.如果H1假设成立,即目标出现机动,DL(k)就呈非零均值的正态分布,但方差仍与式(38)中的相同.其均值由下式给出:
(i)的方差.如果H1假设成立,即目标出现机动,DL(k)就呈非零均值的正态分布,但方差仍与式(38)中的相同.其均值由下式给出:
![]() (39)
(39)
式中![]() ,
,![]() m(i)为机动模型下的滑窗内新息序列.最佳Neyman-Pearson检验由如下似然比确定.
m(i)为机动模型下的滑窗内新息序列.最佳Neyman-Pearson检验由如下似然比确定.
![]() (40)
(40)



评论