基于稀疏信号结构信息的压缩检测算法
首先我们验证本文提出的判决方法的有效性。我们对比不同信噪比下本文提出方法与文献[4]采用的方法的检测成功率,这里部分重构算法我们分别采用文献[4]提出的匹配追踪(MP)算法和改进的压缩采样匹配追踪(CoSaMP)算法,判决方法也分别采用文献[4]的门限判决方法和本文提出的基于信号结构信息的判决方法。令采样点数M=80,信噪比SNR的变化范围为[-10,10],步进为1。实验结果如图1所示。
本文引用地址:https://www.eepw.com.cn/article/203220.htm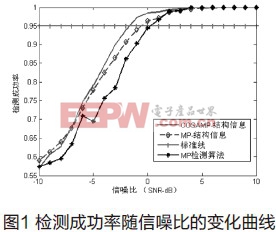
从图1可以看出,本文提出的基于结构信息的判决方法更具优势,同时,采用CoSaMP的部分重构算法比采用MP的部分重构算法获得的结构信息更可靠。下面我们研究测量点数对检测性能的影响。在仿真实验中,我们设迭代次数T=6,固定信噪比SNR=-2dB,图2为仿真实验结果。
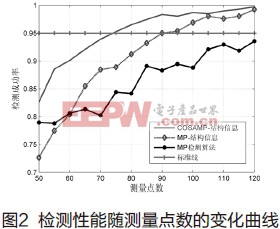
从图中可以看出,提出方法比原有方法更有优势,即使采用原有的部分重构算法,在判决部分采取本文提出方法,检测性能也有所提升。另外,从性能曲线的变化趋势,我们可以看出检测性能随测量点数的增加变得越来越好,这是由于测量点数增多,测量信号中包含的目标信号的结构信息越丰富,部分重构得到的估计信息更可靠。
然后,我们验证迭代次数对检测成功率及检测时间的影响。实验结果如图3和图4所示。
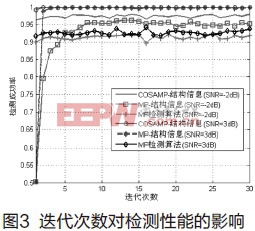
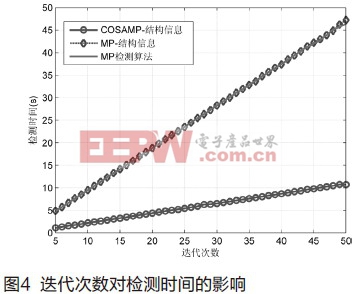
仿真实验中,对于图3所示的实验,我们考虑了SNR=-2dB和SNR=3dB的情况,测量点数为100;对于图4所示的实验,我们设置SNR=10dB,测量点数为100,检测时间定义为1000次检测所用的时间。从图3可以看出,本文提出方法检测性能很稳定,迭代次数对检测性能的影响很小,这是由于采用CoSaMP的部分重构算法在迭代次数很少的情况下就能获得足够的用于判决的结构信息,而采用MP的部分重构算法需要迭代次数达到一定程度时,才能获得可靠的结构信息。另外,从图4可以看出,采用CoSaMP部分重构算法检测方法要比采用MP部分重构算法的检测方法在时间上更有优势,速度更快。综合图3和图4,我们可以得出,本文提出方法在迭代次数很小的情况下也能快速、可靠地检测出目标信号的有无。







评论