探索 Weaver 调制器在单边带调制中的工作原理
使用图形表示来支持我们的数学分析,我们逐步介绍了 Weaver 调制器如何转换信号频率频谱。
本文引用地址:https://www.eepw.com.cn/article/202505/470753.htm与传统的调幅(AM)相比,单边带(SSB)调制在带宽和功率上都有显著的节省。在本文系列中,我们讨论了三种生成 SSB 信号的方法。按照介绍顺序,这些方法是:
滤波法。
相位法。
韦弗方法。
上一篇文章解释了使用单频消息信号的基本原理的韦弗方法。正如我们所学的,韦弗调制器不需要滤波法中使用的锐带通滤波器,也不需要相位法中的精确移相器,使其成为上述三个选项中最实用的一个。图 1 显示了韦弗调制器的电路图。
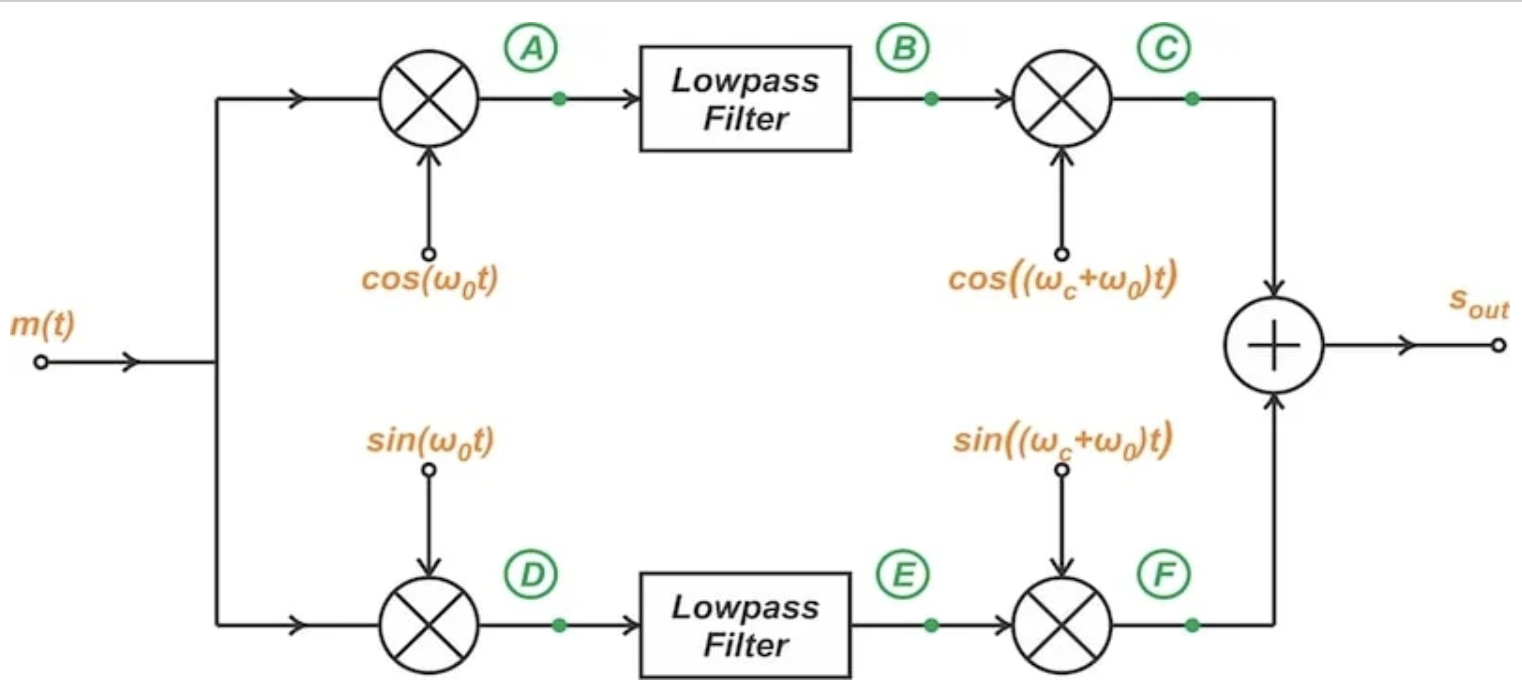
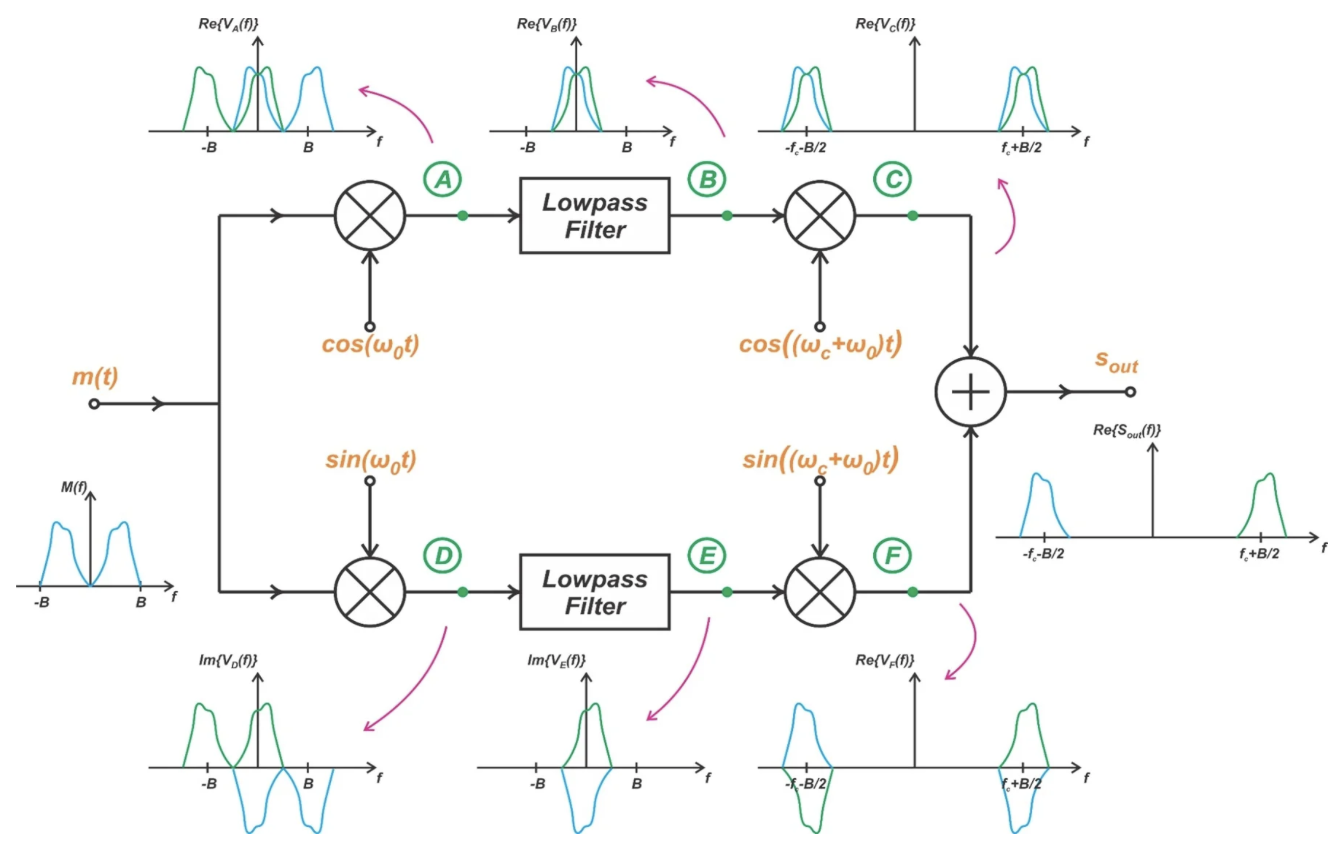
图 1. Weaver 方法生成 SSB 信号。
在本文中,我们将继续探讨该电路,通过检查任意输入频谱如何通过上述图中标出的六个节点——A 到 F——来改变。节点 A 到 C 代表上信号路径;节点 D 到 C 位于下信号路径上。然后,我们将检查通过组合上下路径频谱创建的输出频谱。
图 2 显示了我们的输入频谱,其带宽为 B。
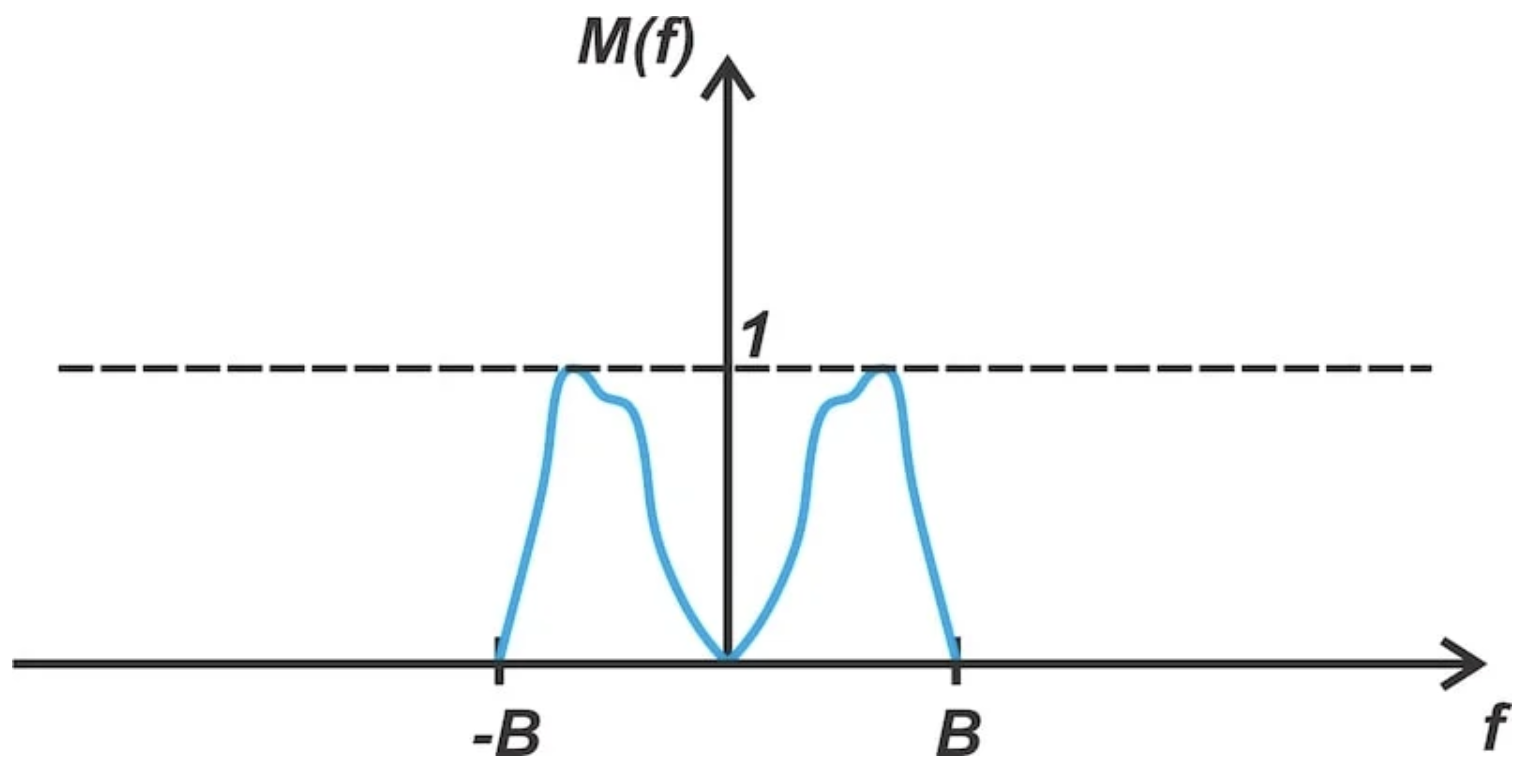
图 2. 用于检查 Weaver 调制器的示例输入频谱。
上行路径:节点 A、B 和 C
让我们首先检查上行路径,它将输入信号与余弦波混合。使用欧拉公式,余弦项可以表示为:
公式 1。
在 Weaver 方法中,第一对乘法器将消息信号与一个振荡器混合,该振荡器的频率(f 0 )位于消息信号频率范围的中心。由于消息信号占据带宽 B,我们有 f 0 = B/2。第一个乘法器因此产生两个信号:一个频谱向上移动 f 0 ,另一个频谱向下移动相同量。在这两种情况下,信号幅度都减半。
图 3(b)显示了该乘法器的输出频谱(电路图中的节点 A)。为了使分析更容易理解,上移和下移的频谱分量用颜色区分:绿色表示下移,蓝色表示上移。
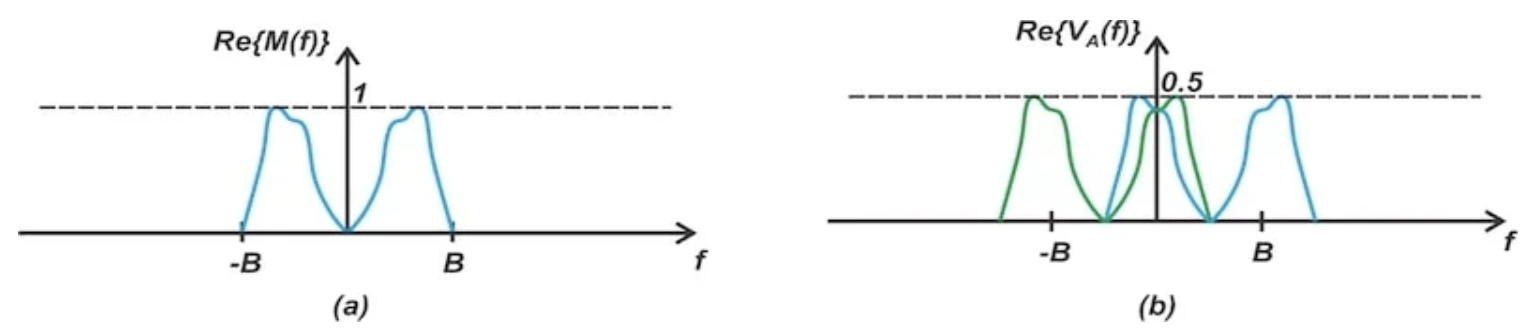
图 3. 上路径中第一个乘法器输入(a)和输出(b)的信号频谱。
图 3 两半的垂直轴均标记为 Re{.},表示这些频谱分量对应于信号频谱的实部。与 Weaver 调制器下路径中使用的混频器不同,输入和节点 A 之间的混频过程不会将输入信号的实部转换为虚部。
从节点 A,信号随后通过一个截止频率为 B/2 的低通滤波器。图 4 显示了滤波器输出(节点 B)处的频谱。
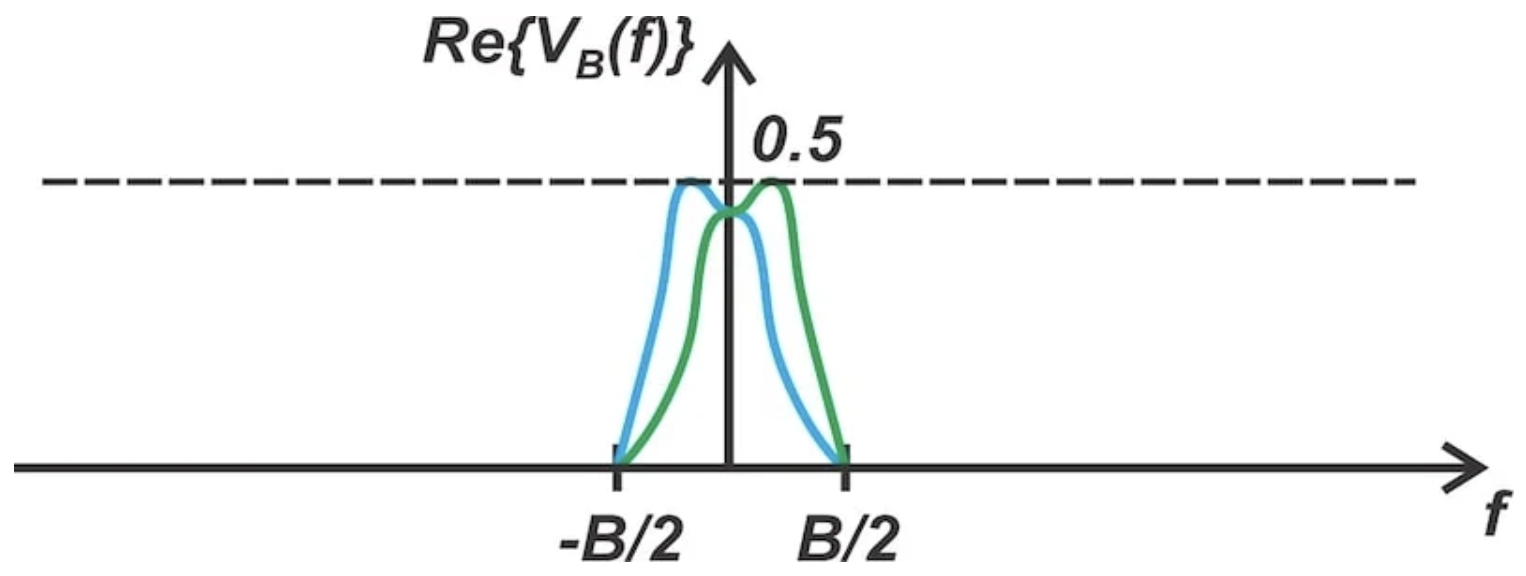
图 4. 节点 B 处的信号频谱,分为上移(蓝色)和下移(绿色)分量。
低通滤波器的输出信号随后被输入到第二个乘法器,在那里它与频率为 f c + f 0 = f c + B/2 的余弦波混合。
类似于我们在第一个乘法器中看到的,上路径的第二个乘法器将频谱平移 ±(f c + B/2),并将幅度再乘以一个额外的因子 0.5,从而相对于输入频谱产生一个整体的缩放因子 0.25。
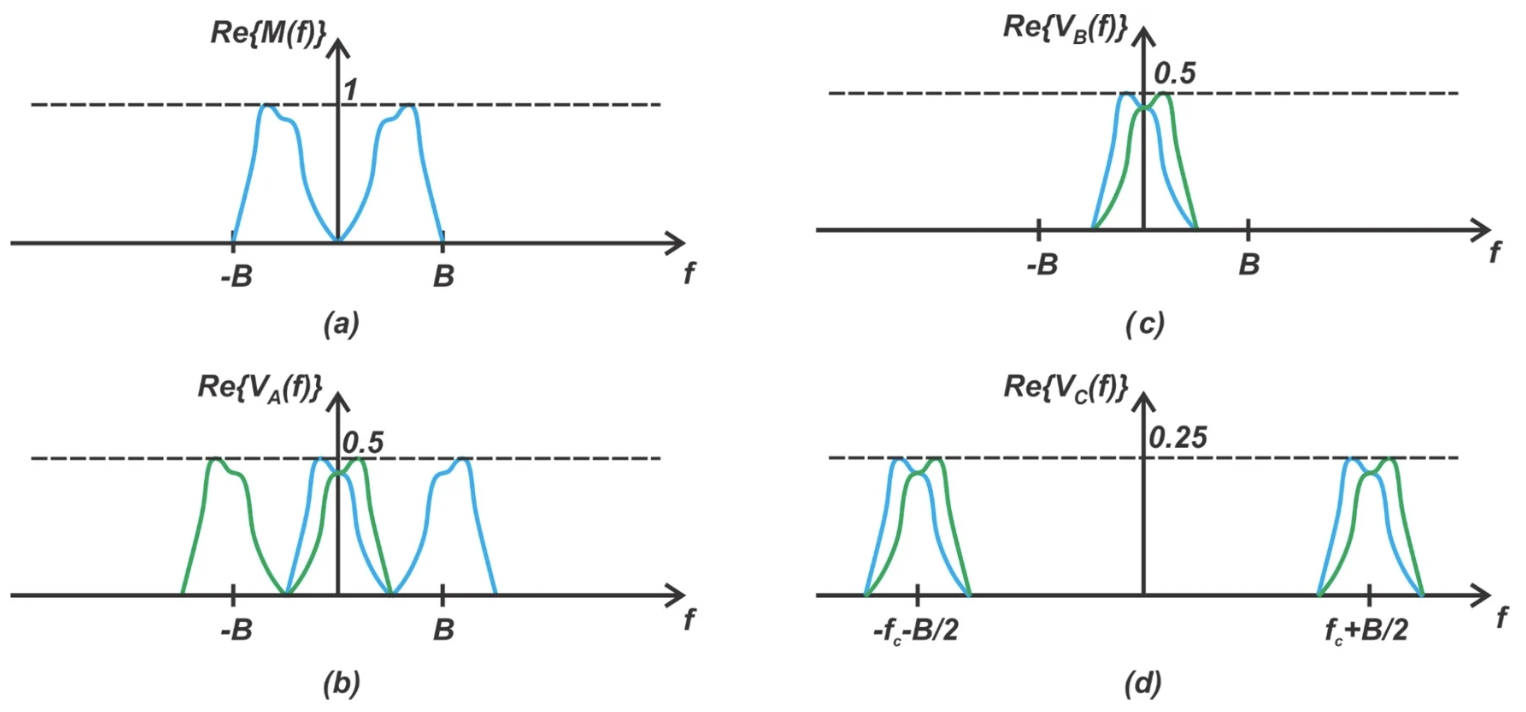
图 5(d) 显示了第二个乘法器(节点 C)的输出频谱。
图 5。Weaver 调制器上路径中不同节点的频谱。[点击放大]
整体而言,图 5 展示了信号频谱如何从输入端通过上路径进行变换。
下路径:节点 D、E 和 F
在大多数方面,下路径的功能与上路径相似。不同之处在于它将输入与正弦波混合,引入了 90 度的相位偏移。使用欧拉公式,正弦函数可以写成:
公式 2.
上移频谱乘以因子 1/(2) = –0.5,而下移分量经历缩放因子–1/(2) = 0.5。虚数单位的存在意味着输入频谱的实部在第一个乘法器(节点 D)的输出处被转换为虚值。结果是图 6(b)中所示的频谱。
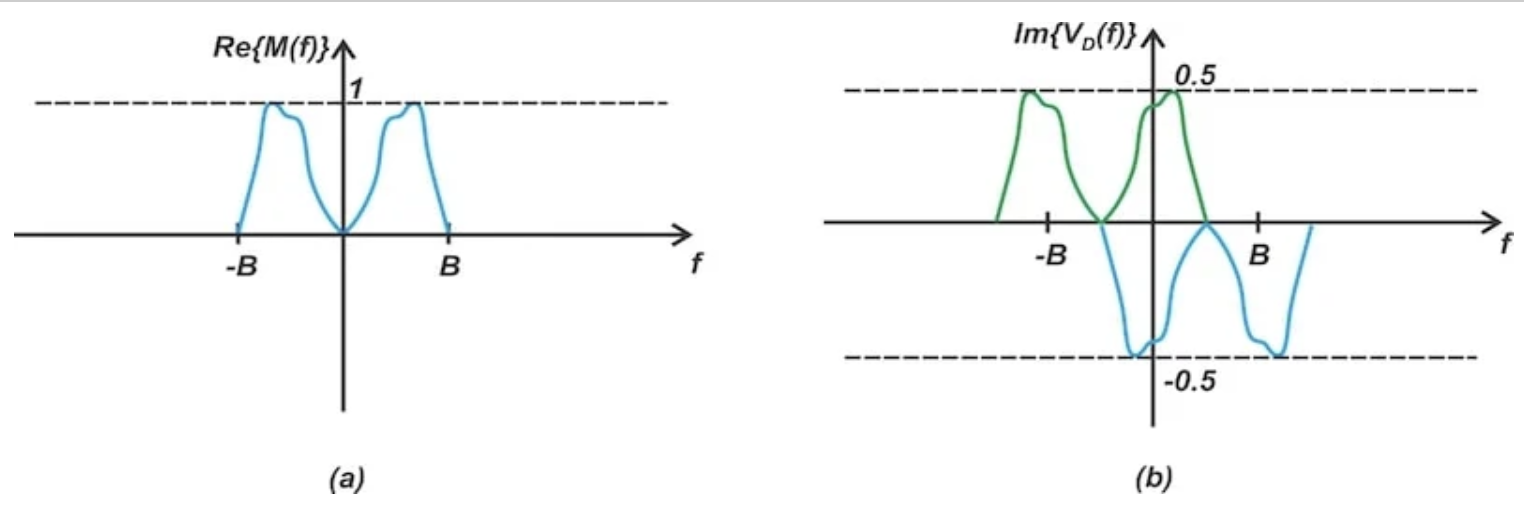
图 6。Weaver 调制器的输入(a)和节点 D(b)处的频谱。
注意,垂直轴从 Re{.}变为 Im{.},表明该图显示了频谱的虚部。
接下来,一个截止频率为 B/2 的低通滤波器消除了其通带之外的所有频率分量。图 7 显示了滤波器输出处的频谱。
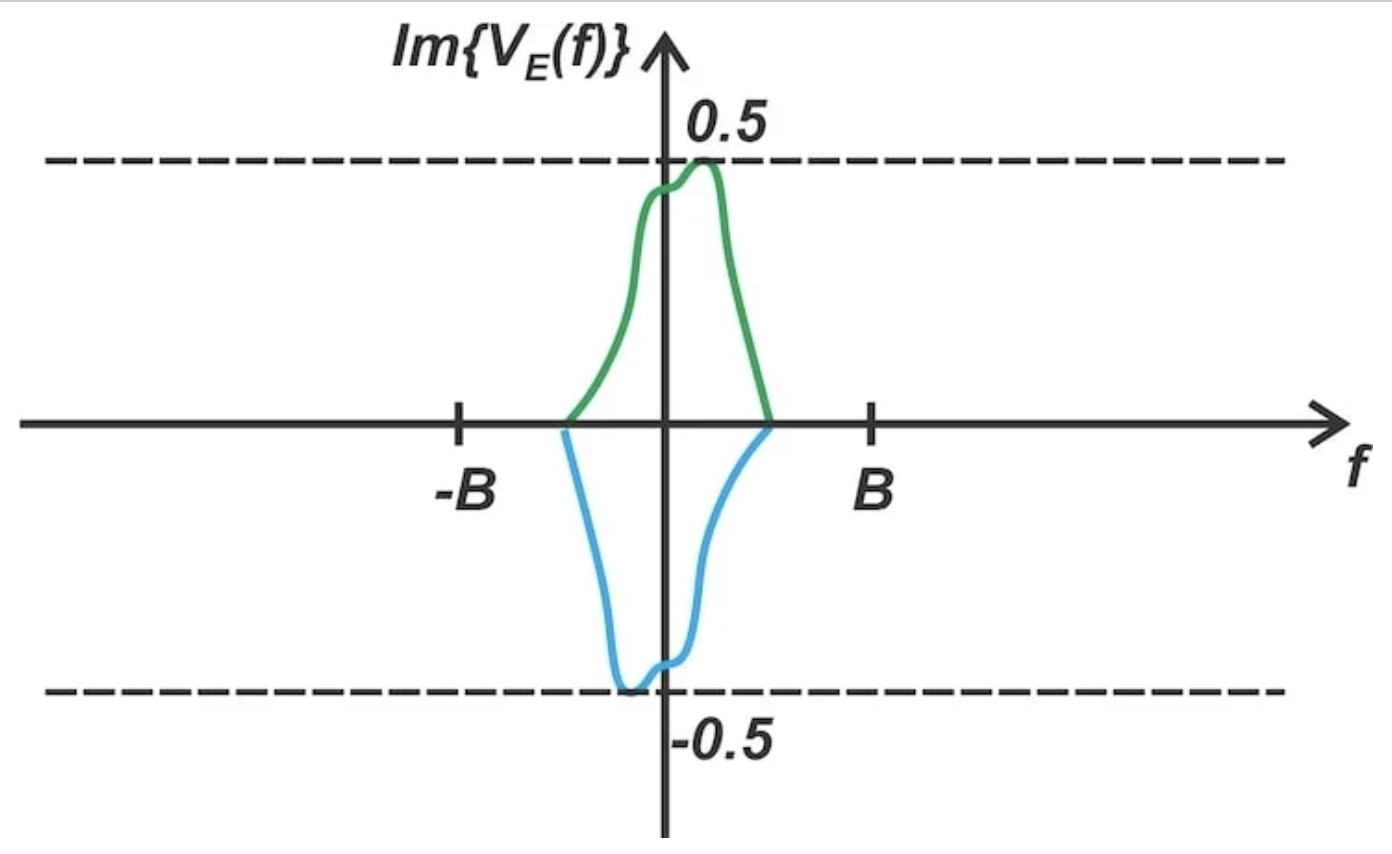
图 7. 下路径滤波器输出端(节点 E)的频谱。
最后,下路径的第二个乘法器将频谱平移±(f c + f 0 ) = ±(f c + B/2)。由于乘以正弦函数,上移和下移的分量幅度分别被缩放-0.5 和+0.5 倍。
然而,施加到第二个乘法器(图 7)的频谱,由于垂直轴旁边的 Im{.}符号,已经有一个隐含的缩放因子。因此,上移和下移的分量分别被缩放-0.5 × = 0.5 和+0.5 × = –0.5 倍。这意味着虚部被转换回实部,如图 8 所示。
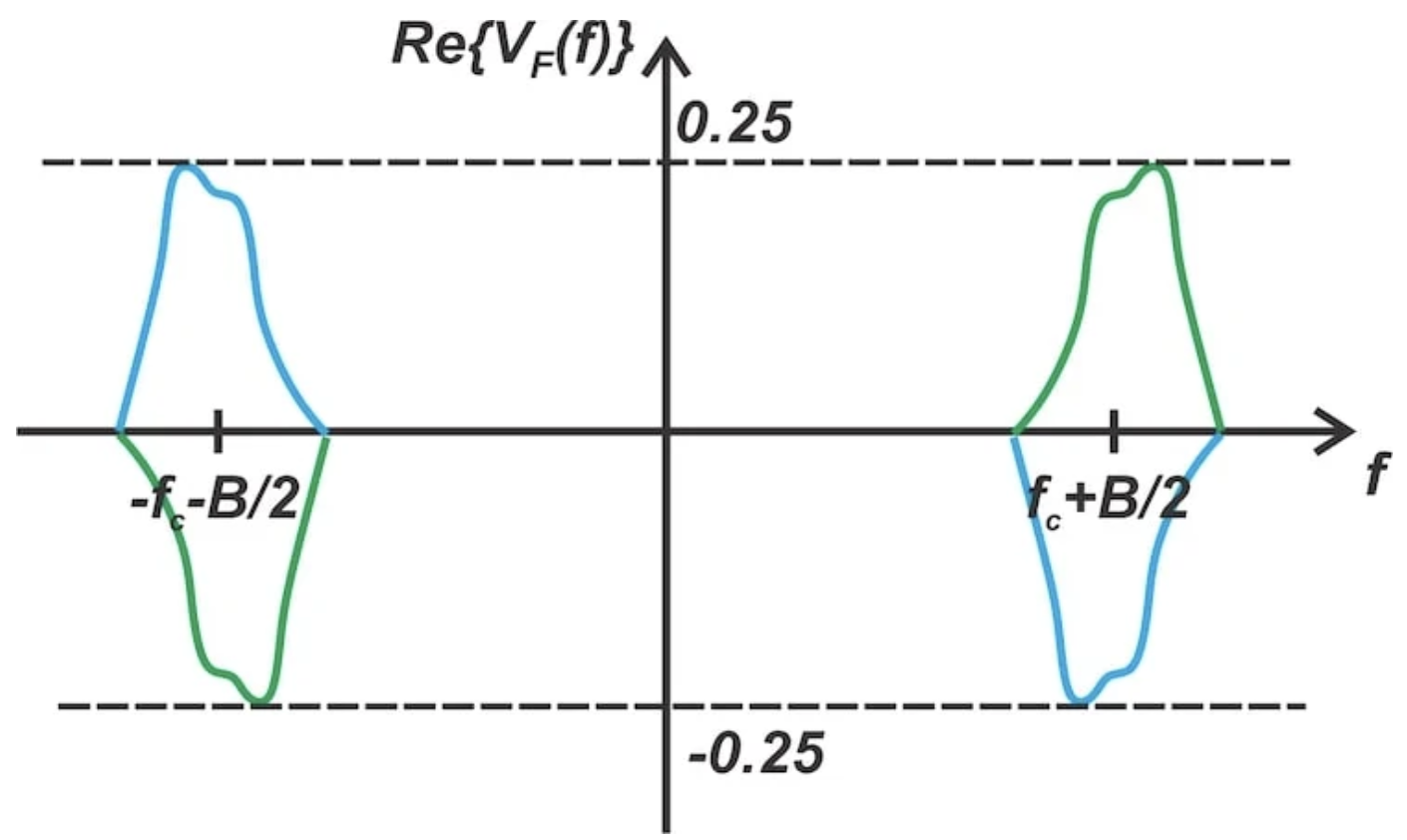
图 8. 下路径第二个乘法器输出端(节点 F)的频谱。
注意到垂直轴已从 Im{.} 变更为 Re{.},表明该图再次显示了频谱的真实部分。
图 9 显示了下方路径所有节点的频谱。
图 9. 从下路径开始到结束的频率谱。[点击放大]
确定输出频谱
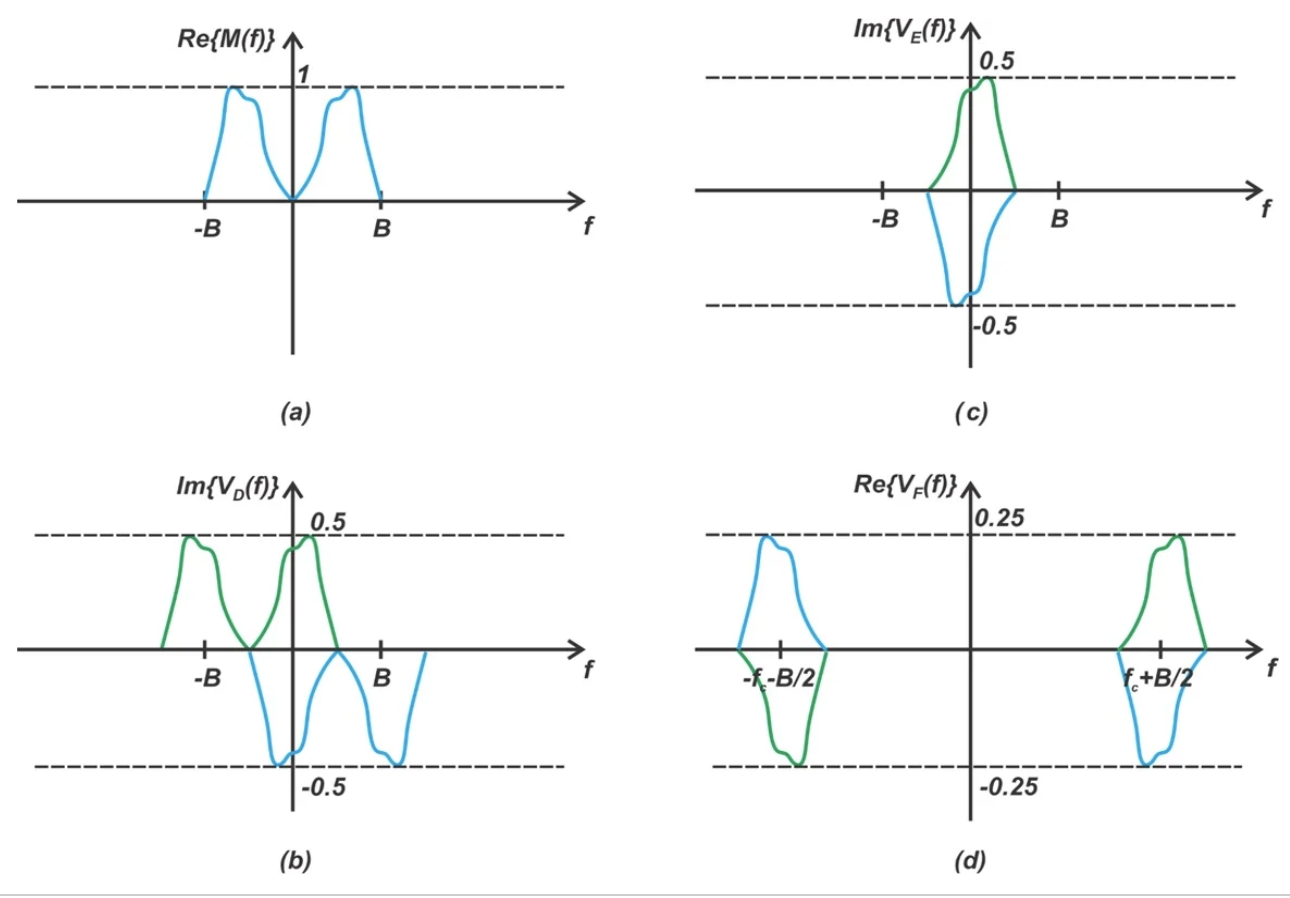
我们通过结合节点 C 和 F 的频谱来获得输出频谱,它们分别代表上路径和下路径的输出。这些频谱可以在图 5(d)和图 9(d)中找到。但是为了帮助我们更容易地可视化,图 10 还重新绘制了这两个频谱以及最终的输出频谱。
图 10. 节点 C(顶部)、节点 F(中间)和调制器输出的频谱。[点击放大]
我们可以看到,上边带在输出端出现。下边带被移除了。
图 11 总结了我们对 Weaver 调制器的分析。它显示了所有节点的信号频谱,包括电路的输入和输出。
图 11. Weaver 调制器所有节点的信号频谱。[点击放大]
下路径节点的另一种表示方法
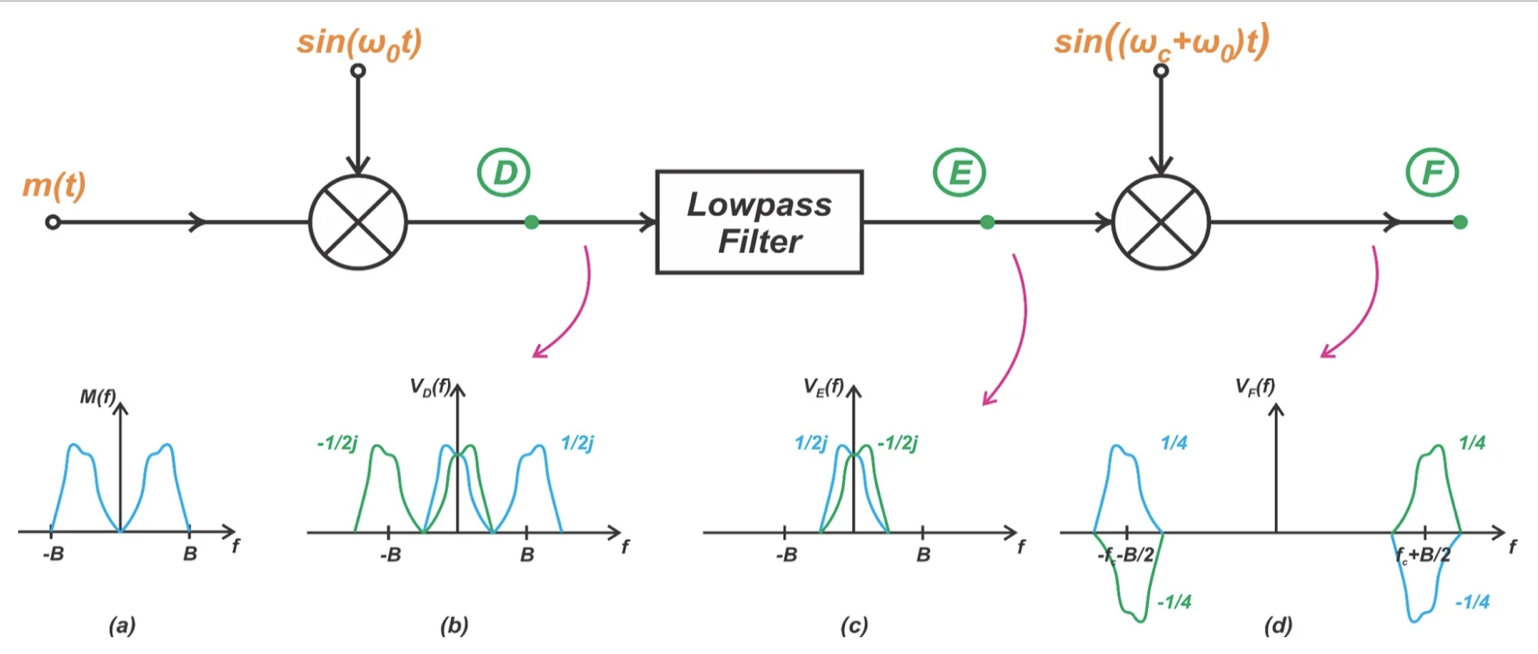
一些作者选择了一种略微不同的方法来表示与下路径相关的频谱分量。他们不是在垂直轴旁边使用 Re{.} 和 Im{.} 符号,而是采用复数缩放因子来表示各种频谱分量。图 12 使用这种方法来显示下路径中节点 D、E 和 F 的频谱。
图 12。下路径不同节点的频谱的另一种表示方法。[点击放大]
为了完整起见,让我们简要使用这种表示方法来验证我们的分析。
由于输入 m(t)与正弦波混合,图 12(b)中的上移频谱分量具有 1/2 的缩放因子。图 12(b)中的下移频谱分量经历-1/2 的缩放因子。低通滤波器消除了高于 B/2 的分量,而不改变缩放因子,产生图 12(c)中的频谱。
最后,下路径中的第二个混频器将图 12(c)中的上移分量乘以 1/2,将下移分量乘以-1/2。由于图 12(c)中的绿色分量已经有一个-1/2 的缩放因子,因此它在图 12(d)中的上移和下移副本分别具有整体缩放因子(-1/2) × (1/2) = 1/4 和(-1/2) × (-1/2) = -1/4。
同样地,图 12(c)中的蓝色分量已经有一个 1/2 的缩放因子。因此,该分量的上移和下移副本将具有整体缩放因子为(1/2) × (1/2) = –1/4 和(1/2) × ( –1/2) = 1/4。比较图 12(d)与图 11,我们看到这个结果与我们的先前分析一致。
总结
在本系列的上一篇文章中,我们通过考虑单频消息信号和应用复基带表示的概念来描述了 Weaver 方法的基础。在本文中,我们使用任意频率谱更深入地探讨了调制器的操作。我希望这些讨论结合起来,能帮助您对这个有用的 SSB 电路建立良好的工作理解。
本文也代表了一个关于射频系统中幅度调制的 15 部分系列的最后一部分。本系列的所有文章的完整列表如下提供。


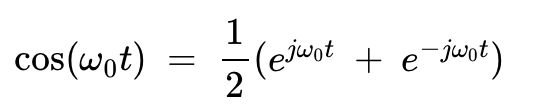
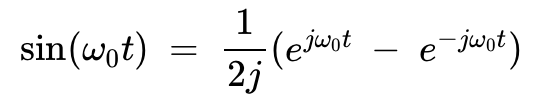


评论