欧姆定律和量子力学之间有什么关系？

欧姆定律是对导体中电压、电流和电阻之间线性关系的经典物理解释。量子力学提供了对这种行为背后的机制的见解，解释了为什么欧姆定律即使在量子效应很重要的非常小的尺度上仍然适用。

欧姆定律是经典物理关系的宏观观点。它通过半经典 Drude 模型扩展到微观尺度，并且可以使用量子计量三角形 （QMT） 在量子尺度上进行检查。

欧姆定律的原始版本是基于实验观察的经验，而不是从基本原理得出的。1827 年，德国物理学家 Georg Simon Ohm 在他的著作“Die galvanische Kette， mathematisch bearbeitet”（《数学研究的电流电路》）中首次发表了该理论。

Drude 模型

Drude 模型是将欧姆定律与基本物理学联系起来的早期尝试。它将欧姆定律的宏观焦点下移至微观层面。它基于金属中相对不动的离子对电子流的散射（图 1）。这是使用麦克斯韦-玻尔兹曼统计对电子气体的动力学理论的应用。

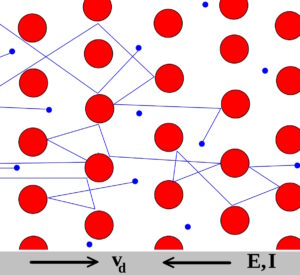
图 1.Drude 模型试图在微观层面上解释欧姆定律。（图片： 维基百科上的数据)

Drude 模型是一个开始，但它有很大的局限性，包括：

• 不考虑温度的影响。

• 不解释高频下的绝缘体或集肤效应。

• 不识别带隙或电子能级的存在。

半经典到量子

Drude 模型基于经典力学。但是，电子以粒子的“气体”形式存在的假设，隐含地认识到它们的量子性质，使该模型成为半经典模型。但是，Drude 模型不包括其他量子效应，例如费米-狄拉克分布和波粒二象性。

在描述欧姆定律时，费米-狄拉克分布的结合很重要，因为它对于理解固体（尤其是金属）中电子的行为以及电子迁移率、能带结构和掺杂效应等现象至关重要。

自由电子模型

自由电子模型，也称为 Drude-Sommerfeld 模型，将经典的 Drude 模型与量子力学费米-狄拉克统计相结合。它仍然是一个简化的模型。它将金属视为自由非相互作用电子的“气体”，但忽略了晶格的影响。

该模型通过将电子视为波并使用费米-狄拉克分布来计算其能级，从而明确包含量子力学效应。它可用于准确预测金属的某些特性，例如导电性和导热性。

自由电子模型通过添加更详细的量子效应得到了改进，从而发展了费米气体和近自由电子模型。

费米气体模型使用理想气体的量子力学版本来支持改进的结果，尤其是在非常低的温度下。近自由电子模型引入了一个弱周期性势来解释固体的晶格结构，并且可以提供更完整的能带和带隙描述。

费米气体模型和近自由电子模型都是改进的，但它们涉及重大简化并且仍然不完整。欧姆定律的理论基础不断发展。

量子计量三角形

虽然理论理解仍在发展中，但 QMT 将欧姆定律的基础牢固地建立在量子电常数之上。该三角形基于电压的约瑟夫森效应、电阻的量子霍尔效应和电流的单电子隧穿。它包含电子电荷 （e） 和普朗克常数 （h） 等基本常数（图 2）。

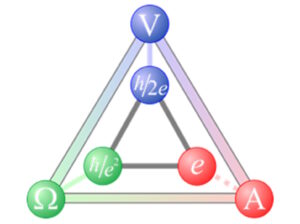
图 2.QMT 将欧姆定律与量子测量相关联。（图片：Metrologia)

QMT 用于在量子尺度上测试和确认欧姆定律。QMT 还提供一种用于高精度测量电子电荷 （e） 和普朗克常数 （h） 的结构。

物理学家使用 QMT 来测试单电子隧穿、约瑟夫森效应和量子霍尔效应的一致性，以及它们与基本常数的关系。最后，QMT 对于 SI 单位系统至关重要，因为它提供了一种使用基本量子现象验证电气单位（伏特、欧姆和安培）的方法。

总结

欧姆定律起源于利用经典物理学概念的经验观察。它的理论基础使用基于量子力学的日益完整的模型不断发展。尽管其理论基础在不断发展，但其实用性已通过 QMT 得到证明，QMT 已在量子尺度上证实了这一点，并已用于验证基本的量子电单元。