基于MATLAB的线性二次型最优控制


对比仿真结果可以看出,当小车摆杆角度权重选定为合适的值,随着小车位置权重的增加,小车位移系统阶跃响应超调减小,上升时间和调整时间也加快。与此同时,也引进了一些振荡。
5.2 加权矩阵R的研究
从降低控制系统能量要求优先角度出发,让Q不变,R减小。这时由Riccati方程求得的系统反馈增益阵K增大。例如R=0.01时,相应的K=[-175.4699,-46.1765,-10.0000,-20.8841]。
改变加权阵Q后的响应结果如图6,控制力输出曲线如图7
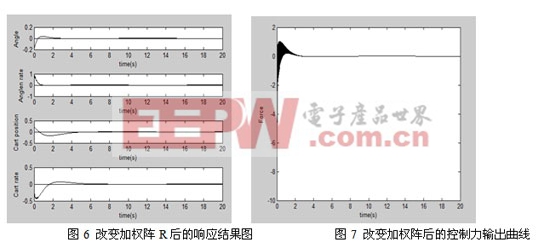
对比仿真结果可以看出,调整时间与超调量减小,上升时间与稳态误差减小。但是系统稳定性很差,时控过程噪声很大。
6 结束语
本文针对倒立摆系统进行数学建模,采用最优控制中的LQR控制方法,对系统进行局部的线性化,通过仿真实验得到该方法作用于倒立摆系统是可行且有效的,同时分析了加权矩阵Q和R对系统性能指标的影响。
参考文献:
[1] 刘金亨,陈今润,吕郁青,等. 基于LQR的一阶直线双倒立摆最优控制系统研究[J].自动化技术与应用,2009,28(5):11-13.
[2] 槐创锋,方跃法. 5连杆双足机器人建模和控制系统仿真[J].系统仿真学报,2008,20(20):82-86.
[3] 李德毅,杜鹚. 不确定性人工智能[M].北京:国防工业出版社,2005.
[4] 姜春瑞. 基于云模型理论的一阶直线倒立摆控制技术研究[D]. 哈尔滨工业大学,2005.
[5] 刘豹. 现代控制理论[M]. 北京:机械工业出版社,2007.
[6] 刘金琨. 先进PID控制及其MATLAB仿真[M]. 北京:电子工业出版社,2003.1.
pid控制相关文章:pid控制原理
pid控制器相关文章:pid控制器原理





评论