基于频率采样法的FIR滤波器的设计及仿真
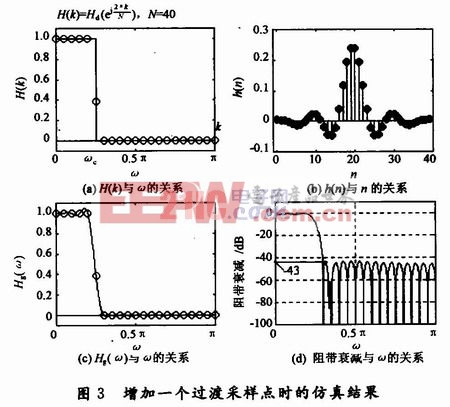
为改进阻带衰减,在边界频率处增加一个过渡点;为保证过渡带宽不变,将采样点数增加一倍,变为N=40,并将过渡点的采样值进行优化,取H1=O.390 4,其仿真结果如图3所示。由图3(d)可见,这时阻带衰减达到了-43 dB。
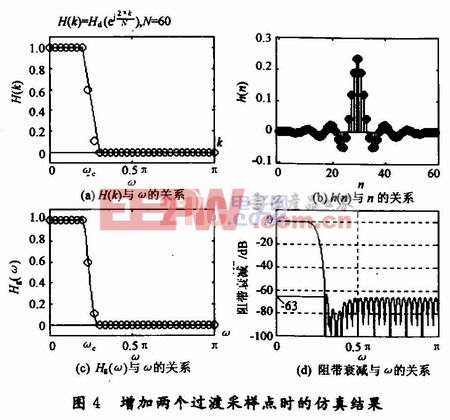
为进一步增加阻带衰减,可再增加一个过渡采样点,并将采样点数增加到60。两个过渡样点值经优化分别为H1=O.592 5和H2=O.1099,其仿真结果如图4所示。由图4(d)可见,这时阻带衰减达到-73 dB。还可以通过进一步增加过渡样点来增加阻带衰减,一般情况下,最多增加3个过渡采样点即能满足阻带衰减的要求。显然,在保证过渡带宽不变的情况下,相应的采样点数也成倍增加,这样将使滤波器的复杂度大大增加,在实现滤波时计算量也随之增加。
4 结语
Matlab仿真结果验证了用频率采样法设计FIR线性相位数字滤波器这一数字信号处理中的基本理论,有助于学生深入理解并掌握这一重要的FIR滤波器设计方法。需要强调的是,频率采样法是从频域出发直接设计滤波器的,而窗函数法是从时域出发设计滤波器的,两种设计方法各有优缺点。窗函数法设计FIR数字滤波器是傅里叶变换的典型运用,而频率采样法设计的指导思想是频域采样定理及内插公式,其阻带衰减的改善是通过增加过渡采样点实现的,同时为保证过渡带宽的不变,滤波器的采样点数也要相应增加,计算复杂度也随之成倍增加,这就要求在用频率采样法设计FIR滤波器时,要综合考虑阻带衰减和滤波器长度的要求,从而达到设计的最优化。









评论