基于频域滤波数字均衡器的设计
加入技术交流群
2．2．2 蝶形运算的算法
蝶形运算是逐级运算累加实现的，在传统的蝶形运算中，旋转因子
的N是保持一个固定的值而k是不断变化的，第一级到第
级中，k的变化是以2为底的幂指数的变化，而到第
级时，k的变化则是0，1，…，(N／2)-1。如果依照k的这种变化规律，在第级时，就很难继续依照前级进行变化。因此，根据以上分析，采用另外一种思路来对蝶形运算进行重新的整理。在旋转因子中，N是每个蝶形单元输入数据的个数，k的变化规律是0，1，…，(N／2)-1，采用这种方法就可以有效的缩短代码的长度，提高运行速度。图1为蝶形运算流程图。本文引用地址：https://www.eepw.com.cn/article/187578.htm
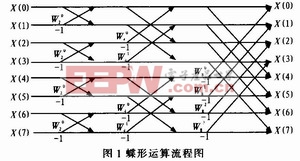
2．3 快速傅里叶变换的实现
蝶形运算的旋转因子
，输入的复数表示为InputData=RealInData+j*ImagInData，因此在计算过程中，旋转因子和输入数据的计算过程是将实数和复数分开计算所得到的。
因为旋转因子中k=0，1，…，(N／2)-1，因此随着k的增长cos(-2Pik／N)和sin(-2Pik／N)也相继发生成倍的变化。
对这一现象采用的处理方法是使用正余弦的倍角公式：
这样，处理的变化的过程就变为处理正弦和余弦倍角变化的过程，从而简化了程序。部分程序如下：
其中，Block是每一个蝶形单元输入个数的一半即N／2，r0和i0分别是旋转因子的实部和虚部。
评论