双极发射极跟随器：具有双通道反馈的RISO

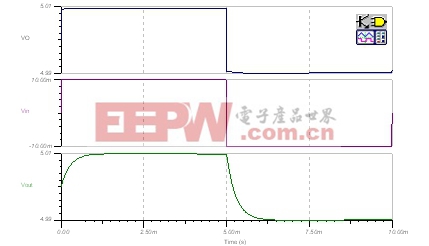图27：最终瞬态稳定性测试：发射极跟随器。

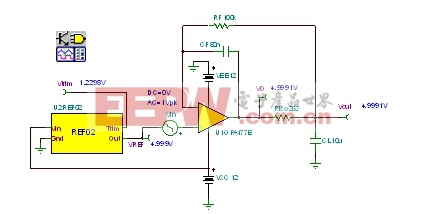通过图28中的Tina SPICE电路，可验证我们对Vout/Vin的推算是否正确。

从图29中，我们可以看出，Vout/Vin的测试结果与我们推算的一阶分析结果一致，具体表现为：当频率为625.53Hz时，单极点开始下降。而且，当频率约为200kHz(此时，FB#2与OPA177 Aol曲线相交)时，出现第二个极点。

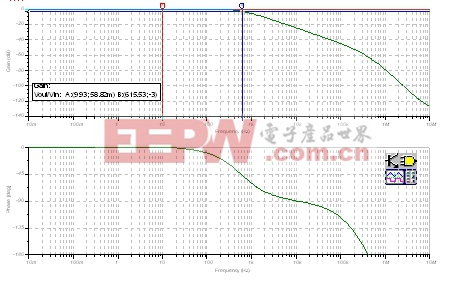图29：最终Vout/Vin传输函数：发射极跟随器。

图30总结了一种易于使用的渐进式程序。这种程序轻松地将具有双通道反馈的RISO电容性负载稳定性技术应用于双极发射极跟随器输出运算放大器上。

1. 测量运算放大器的Aol。
2. 测量运算放大器的Zo，并在图上绘制出其曲线。
3. 确定RO。
4. 创建Zo的外部模型。
5. 计算FB#1低频1/b：对单位增益电压缓冲器而言，该值为1。
6. 将FB#2高频1/b设置为比FB#1低频1/b高+10dB(为获得最佳的Vout/Vin瞬态响应并实现环路增益带宽相移量最少)。
7. 从FB#2高频1/b中选择Riso以及RO。
8. 从CL、Riso、RO中，计算FB#1 1/bfzx。
9. 设置FB#2 1/b fza=1/10fzx。
10. 选择具有实际值的RF和CF，以产生fza。
11. 采用Aol、1/b、环路增益、Vout/Vin以及瞬态分析的最终值，运行仿真以验证设计的可行性。
12. 核实环路增益相移的下降不得超过135度(>45度相位裕度)。
13. 针对低噪声应用而言：检查Vout/Vin扁平响应，以避免增益骤增→Vout/Vin中的噪声陡升。

图30：具有双通道反馈的RISO补偿程序：发射极跟随器。

图31：双通道反馈和BIG NOT。

当运算放大器采用双通道反馈回路时，有一种异常重要的情况需要避免，那就是“BIG NOT”。如图31所示，存在能够产生反馈回路的运算放大器电路(反馈回路导致了BIG NOT)，这可从包括有效1/β斜坡(从+20db/decade骤变为-20dB/decade)的最终1/β曲线中看出。这种快速变化意味着在1/β曲线中存在复共扼极点，因此，也意味着在环路增益曲线中存在复共扼零点。当处于复合零点/复合极点的频率时，复合零点和极点产生了±90度的相移。同时，在复合零点/复合极点附近的相位斜坡在频率发生位置的窄频带，可在±90度至±180度之间变化。出现复合零点/复合极点将在闭环运算放大器响应中导致增益的骤增。这种现象会造成负面的影响，尤其是对于功率运算放大器电路而言，更是如此。

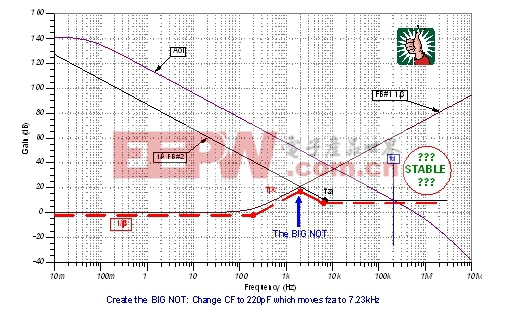图32：以图表的形式创建BIG NOT。

让我们回到图17OPA177 Aol曲线上的FB#1和FB#2标绘点，只要改变如图32所示的fza的位置，就可轻而易举的创建BIG NOT。在fcl处，按照以往接近速率的情况，显示这种电路的运行是稳定的——但是，果真如此么？

在图33中，我们改变了同时用于分析FB#1和FB#2的Tina SPICE电路，以创建如图32所示的BIG NOT。将CF由82nF调整为220pF，以便于将fza移到所需的BIG NOT创建位置。

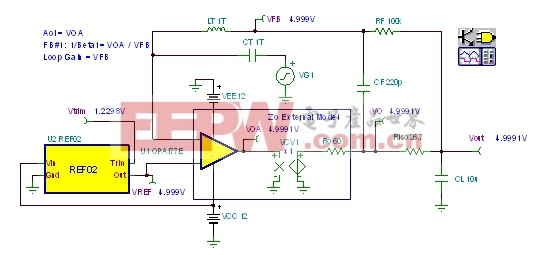图33：环路增益分析电路：BIG NOT。

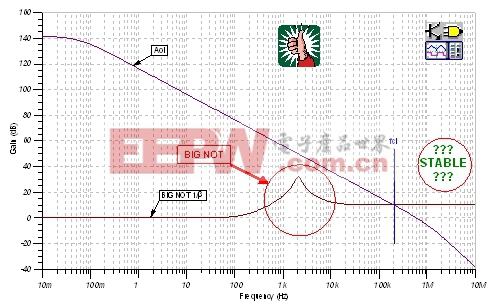图34：1/β曲线：BIG NOT。

BIG NOT的1/β曲线与OPA177 Aol曲线一起在图34中标绘出来。在fcl处，出现了20dB/decade的接近速率。但是，请注意在BIG NOT1/β曲线中，斜率有一个急剧的变化--从+20dB/decade变为-20dB/decade。然而，这种1/β曲线的急剧变化并非是一件好事，为此，我们应质疑这种电路的稳定性。

图35中BIG NOT电路的环路增益曲线表明相移几乎达到了180度(当频率为1.034kHz时，大于167度)，这意味着当频率为1.034kHz时，我们仅与180度的相移相距约13度。同时，请注意观察在这同一区域，环路增益是如何向下朝着零点环路增益急剧形成尖峰的。同样，在fcl处，有着充足的相位裕度。但是，我们还是会问，这种电路运行稳定么？

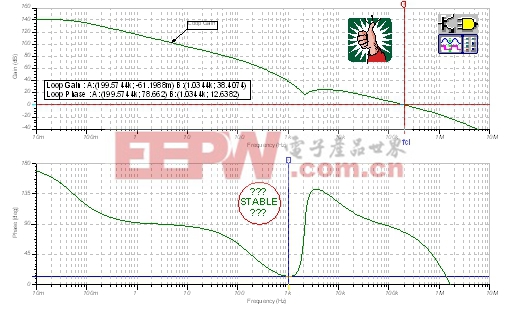图35：环路增益分析：BIG NOT。

于是，假设我们在稳定性分析技巧方面毫无经验(事实上并非如此)，接着构建这款BIG NOT电路。我们期望了解实际应用中的瞬态稳定性会是如何开展的。通过图36中的Tina SPICE电路，我们可以看到，如果我们将该BIG NOT电路投入量产，再将其投入实际的应用中，会产生什么结果呢？

千万不要告诉您的上司，我们将该电路投入了量产，否则情况会更糟糕。客户收到您发送的、内置这种电路的设备后，发现有时向电路供电或当其他负载突然馈入该参考缓冲电路时，会出现奇怪和间歇性的问题。这是更新我们的历史参数的适当时候吗？尽管该电路不是振荡器，但是，如图37所示来自瞬态稳定性测试中过度的振铃和很长的建立时间意味着电路处于稳定的边缘上。根据BIG NOT出现的位置，振动器振铃的持续时间和振幅更容易变得比本例所述的情况还糟。从电路板和系统层面来考虑，我们将这种电路定义为“不稳定”，尤其是当我们的分析工作未涵盖实际应用中的寄生效应时，情况更是如此(这些寄生效应出现在PCB布局、组件容差、运算放大器参数容差以及组件和运算放大器参数的温度变化等方面)。令人感到欣慰的是，我们只将该电路投入“虚拟”的量产，而相应的将我们的具有双通道反馈的RISO应用到即将投入实际使用的电路。

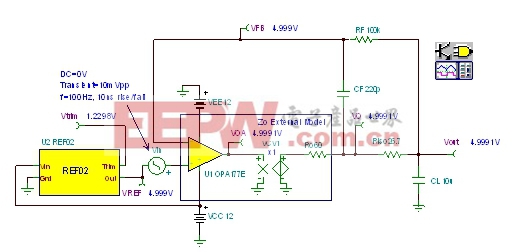图36：瞬态稳定性测试电路：BIG NOT。

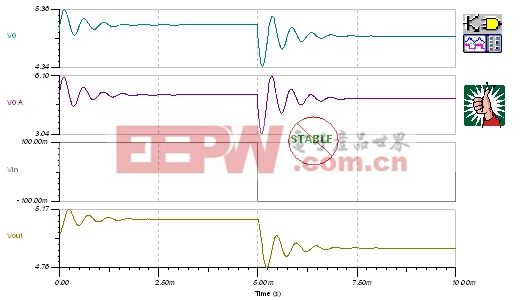图37：瞬态稳定性测试：BIG NOT。

CMOS RRO：具有双通道反馈的RISO

我们选择用于分析具有双通道反馈的RISO的CMOS RRO为OPA734，具体情况请参阅图38。OPA734是一款低漂移、低输入失调电压的运算放大器，其能在+2.7V～+12V的电压范围内工作。这种极低的漂移(0.05uV/C)加上其超低的初始输入失调电压(1uV)，使OPA734成为了单电源应用中理想的参考缓冲放大器。由于这并非是轨至轨CMOS输入放大器，因此，我们有必要观察输入电压范围的技术规范[(V-)-0.1V至(V+)-1.5V]。

图38：CMOS RRO运算放大器的技术规范。