双极发射极跟随器:具有双通道反馈的RISO
通过如图9所示的Zo外部模型,我们能够测量Zo与Riso、CL、RF以及CF之间相互作用对1/β的影响。在Zo外部模型中,设置Ro=Ro OPA177,实际测量值为60欧姆。压控电压源VCV1将运算放大器宏模型U1从Ro、Riso、CL、CF以及RF中隔离开来。将VCV1设置为x1,以确保产品说明书中的Aol增益不变。由于我们要在稳定性状况最糟的情况下(只存在CL以及我们计算得出的空载Zo[此时Ro=60欧姆])分析这种电路,因此,务必排除各种大的DC负载。VOA是一个与运算放大器相连的内部节点,在实际工作中,我们无法实现对这种节点的测量。同时,许多SPICE宏模型上的这种内部节点接入,也并非易事。对1/β进行分析(相对于VOA),已涵盖了Ro、Riso、CL、CF以及RF的影响。如果未采用Zo外部模型,SPICE中的最终稳定性仿真就无法标绘出1/β的曲线;但是,如果采用Zo外部模型,则可标绘出环路增益的曲线以确认我们分析的正确性。
首先,我们要分析如图10所示的FB#1。请注意,由于我们只分析FB#1,所以CF可视为处于开路状态。接下来,我们将分析FB#2。然后,通过采用叠加的方法,将两条反馈通道合并在一起,求取最终的1/β。分析结果如图上所示,有关的公式推导和具体细节,请参阅下一张图(图11)。我们发现,当fzx=183.57Hz时,FB#1 1/β曲线的增益为零。低频1/β值为1。如欲获得该增益,那么低频1/β值应大于1。
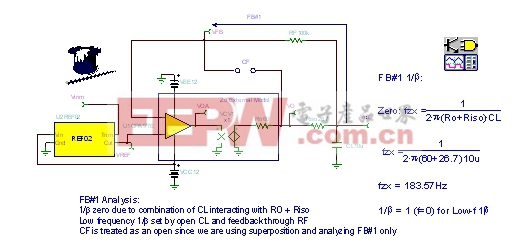 |
| 图10:FB#1分析:发射极跟随器。 |
 |
| 图11:FB#1 1/β公式的推导:发射极跟随器。 |
FB#1β的公式推导如图11左侧所示。由于1/β是β的倒数,所以FB#2 1 1/β的计算结果可以轻而易举的被推导出来,具体推导过程,请参阅图11右侧。从图中我们还发现,在β推导过程中的pole,fpx变成了1/β推导过程中的zero,fzx。 我们将采用如图12所示的电路来开展AC分析:通过Tina SPICE,求取FB#1的1/β,OPA177的Aol以及只采用FB#1电路的环路增益。正因为如此,所以我们将CF从图中除去。
FB#1 1/β的结果标示在图13中的OPA177 Aol曲线上。在环路增益为零的fcl处,我们发现,接近速率为40dB/decade:[(Aol曲线上的-20dB/decade)-(FB#1 1/β曲线上的+20dB/decade)=-40dB/decade接近速率)]。
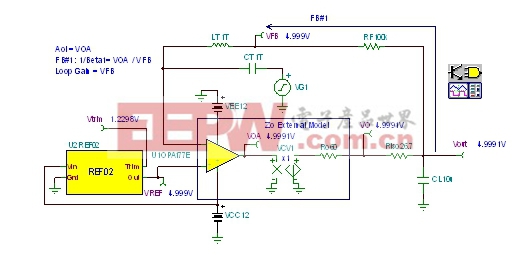 |
| 图12:FB#1AC电路分析:发射极跟随器。 |
接近速率的经验数据表明了存在的不稳定性。我们对FB#1的分析是基于zero、fzx=183.57Hz,低频1/β=1的情况。从图13中可以看出,我们的一阶分析准确地推算出了FB#1 1/β的数值。
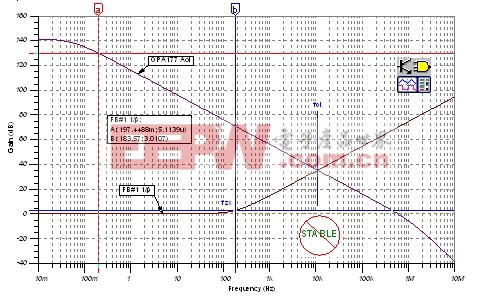 |
| 图13:FB#1 1/β曲线图:发射极跟随器。 |
从图14中我们发现,只配置FB#1的电路环路增益分析显示,在环路增益为零的fcl处,相位裕度接近零。这样,就明确证实了电路的不稳定性。通过检测图13中Aol曲线上的FB#1 1/β曲线,可推算出环路增益曲线上的极点和零点。
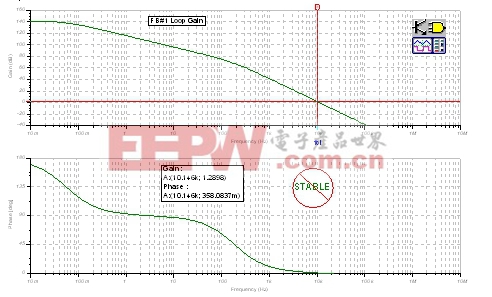 |
| 图14:FB#1环路增益分析:发射极跟随器。 |
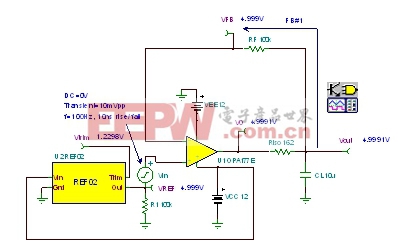 |
| 图15:FB#1瞬态稳定性测试电路:发射极跟随器。 |
如果我们有任何疑问,或如果只采用FB#1构建参考缓冲电路,此时,我们可运用如图15中的电路,进行实际的瞬态稳定性测试。
图16中的瞬态稳定性测试结果同时与Aol曲线上的1/β值和环路增益曲线一致,因此,证明了只采用FB#1构建参考缓冲电路,将导致电路运行的不稳定性。
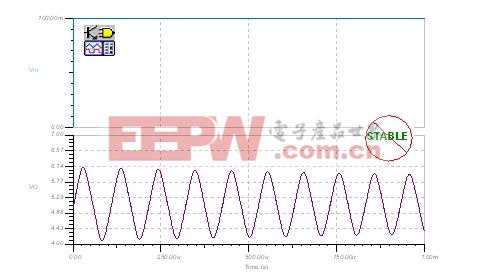 |
| 图16:FB#1瞬态稳定性测试:发射极跟随器。 |
现在,我们必须弄清楚如何生成一款解决方案,以保证电容性负载参考缓冲电路的稳定性。此时,我们进一步了解了如图17所示的Aol曲线和FB#1 1/β曲线。如果我们添加如图17所示的FB#2 1/β曲线,我们则会看到一条最终的1/β曲线,这样,根据fcl处的接近速率以往的稳定性经验,我们可以推断电路的运行也将是稳定的。
另外,我们将促使fpc低于1/β曲线中的fzx一个decade,以确保当频率低于fcl时,相位裕度优于45度。上述工作通过调整1/βFB#2的高频部分,使其比FB#1低频1/β高出+10dB。然后,设置fza,使其至少低于fpc一个decade,以确保当实际应用中进行参数变化时,能够避免BIG NOT。通过观察,我们发现,最终的1/β曲线是在FB#1 1/β曲线和FB#2 1/β曲线中选择最小数值的1/β通道而形成的。
务必请记住,在双反馈通道中,从运算放大器输出端至负极输入端的最大电压反馈将主导着整个反馈电路。最大的反馈电压意味着β值最大或者是1/β值最小。图18向我们展示了这种关键的推算技巧。
最后,在FB#2取得支配地位之前,预计Vout/Vin的传输函数将随着FB#1的变化而变化。此时,Vout/Vin将会衰减至-20dB/decade,直至FB#2与Aol曲线相交,然后,将随着Aol曲线下降。
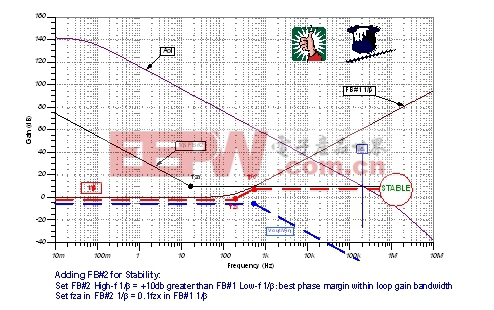 |
| 图17:FB#2图解分析:发射极跟随器。 |
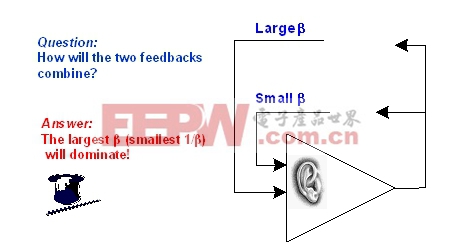 |
| 图18:双通道反馈、叠加以及1/β:发射极跟随器。 |
图18告诉我们,当整个运算放大器电路采用双通道反馈电路时,最大的β值电路将居支配地位。一个很明显的例子就是,如果有两个人对着您的同一只耳朵讲话,您会更易于听到哪个人的讲话?当然是嗓门最大的那个人!同样的道理,运算放大器也将会“听到”β值最大或1/β值最小的反馈电路。运算放大器察觉到最终的1/β曲线将是在各种FB#1 1/β或FB#2 1/β频率时,频率较低的那一条曲线。
如图19所示,里面会有一些主要的假设。我们将这些假设运用于几乎所有的具有双通道反馈的RISO电路中。首先,我们假设CL>10*CF,这也就是说,在高频率时,CL早在CF短路前短路。因此,我们将短路CL以排除FB#1,从而便于单独分析FB#2。另外,我们假设RF>10*Riso,这意味着作为Riso的负载,该RF几乎完全失效。从图19和图20中具体的公式推导,我们可以看出,当zero,fza=19.41Hz(由RF和CF产生)时,FB#2在原点拥有一个极点。由于在高频时,CF和CL同时处于短路状态,所以FB#2高频1/β部分即为Ro+Riso与Riso之间的比值。FB#2 1/β的公式推导请参阅下一张图(图20),有关计算结果请参阅下图。FB#2高频1/β设置为3.25dB或10.24dB、原点拥有一个极点以及当频率为19.41Hz时的零点。
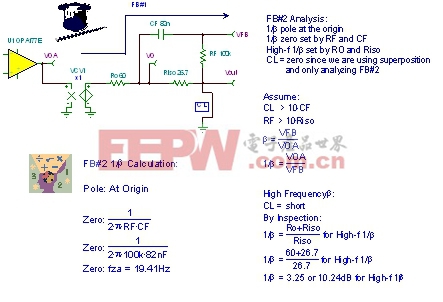 |
| 图19:FB#2分析:发射极跟随器。 |
 |
| 图20:FB#2 1/β公式推导:发射极跟随器。 |
FB#2β的公式推导如图20左侧所示。由于1/β是β的倒数,所以FB#1 1/β的计算结果可以轻而易举的被推导出来,具体推导过程请参阅图20右侧。从图中我们还发现,在β推导过程中的pole,fpa变成了1/β推导过程中的zero,fza。
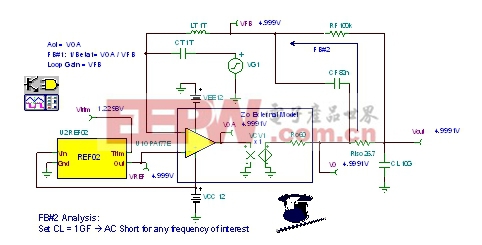 |
| 图21:FB#2AC电路分析:发射极跟随器。 |
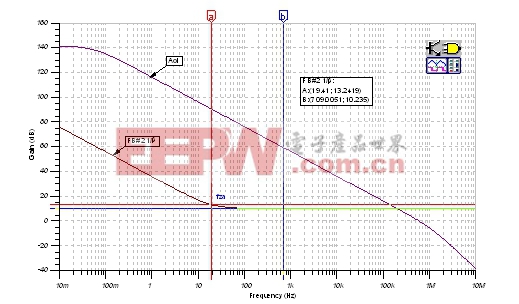 |
| 图22:FB#2 1/β曲线:发射极跟随器。 |
为了检验FB#2的一阶分析情况,我们可采用如图21所示的Tina SPICE电路。再者,为了便于分析,我们将CL设置为10GF,因此对各种相关的频率而言,CL都等同于短路状态。但是,在开展AC分析前,仍允许SPICE查找到相应的DC工作点。
Tina SPICE仿真的结果如图22所示。FB#2 1/β曲线正如当fza=19.41Hz以及高频1/β=10.235dB时,采用一阶分析推算出来的结果一样。另外,我们也绘制出OPA177 Aol曲线,以弄清楚在高频率时,FB#2将如何与其相交。
如果推算的FB#1和FB#2的叠加结果会产生所需的最终1/β曲线,那么我们将通过如图23所示的Tina SPICE电路,开展分析工作。我们还可通过Tina SPICE电路,绘制出Aol曲线、最终的1/β曲线以及环路增益曲线。
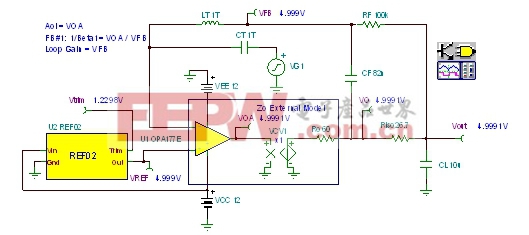
| 图23:最终环路增益分析电路:发射极跟随器。 |
从图24中,我们可以看出,分析结果验证了我们所推算的最终1/β曲线。在环路增益为零的fcl处,推算的接近速率为20dB/decade。
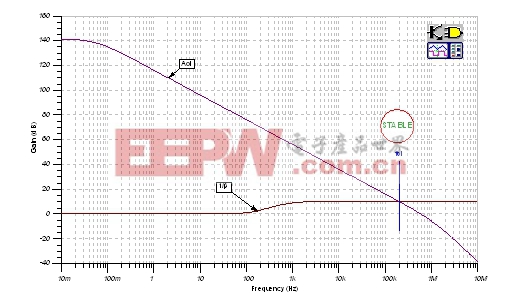 |
| 图24:最终1/β曲线:发射极跟随器。 |
最终电路的环路增益相位曲线(采用FB#1和FB#2)如图25所示。相移从未下降至58.77度以下(如为当频率为199.57kHz时的情况),而且,在fcl处(频率为199.57kHz),相位裕度为76.59度。
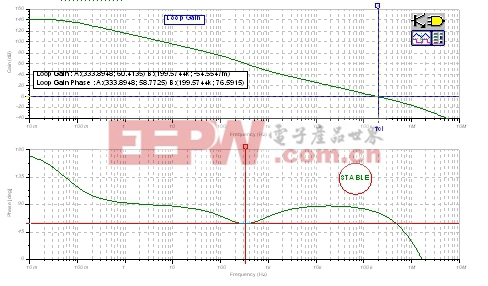 |
| 图25:最终环路增益分析:发射极跟随器。 |
我们将采用图26中的Tina SPICE电路,对我们的稳定电路进行最后的检验-瞬态稳定性测试。
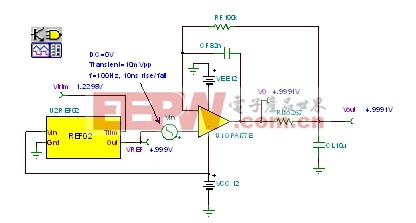 |
| 图26:最终瞬态稳定性测试电路:发射极跟随器。 |



评论