基于ADS的接收机码元同步算法实现
加入技术交流群
假设接收信号为：
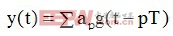，式中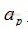
为传输的复数数据，
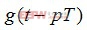为基带成型滤波波形，对
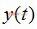的采样值可能产生定时误差，Gardner算法提取的定时误差为：
（2-1）其中索引r表示符号数目，同相I和正交Q方向的第r个符号的判决值分别表示为
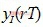和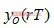
。同样，将r和（r-1）两个判决点中心位置的采样值表示为
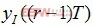和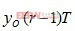
。整个误差是I和Q两个方向的定时误差之和，且此误差与载波相位无关。式中
,
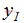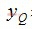表示同相和正交分量，T为符号周期。Gardner算法适用于跟踪和捕获模式。本文引用地址：https://www.eepw.com.cn/article/185592.htm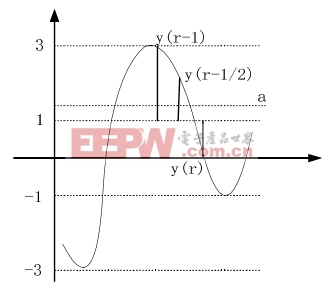
图3 16QAM解调后波形
在 16QAM调制信号中，例如果符号从－1变为1，1变为－1，－3变为3，3变为－3等的时候，则没有定时误差时，中间点的平均值应为零。而有定时误差时，将会产生一个非零的值，它的大小与差错的大小成正比。另外一些情况，当没有定时误差时，中间点的平均值并不是零。例如符号从3变为－1，当没有定时误差时，中间点的平均值是1，如图3所示。
如果直接把Gardner算法运用在16QAM解调系统中，定时误差检测的结果有些点上是正确的，有些点上是错误的。对于大量数据，这些错误的平均值是零，因为没有定时误差的情况，中间点可能是0，－1，1，－2，2，其平均值为零。因此这些错误会导致定时时钟的抖动，通过滤波器可以减小这些抖动。
为了消除这些抖动。我们对Gardner算法做了进一步改进，其改进后算法为：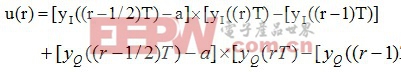
（2-2）
其中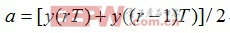
当定时超前，误差为负，定时滞后，误差为正。Gardner算法具有两个特点：一是每个符号只需要两个采样点，且以码元速率输出误差信号；二是估计算法是独立于载波相位的，不受载波相位偏移的影响，即可以在载波相位同步之前，进行定时误差估计。
评论