实现电流零纹波的耦合电感计算

L_eP→∞，L_eS=L₂其效果是使原边纹波电流为零，副边纹波不变。

这可以解释为：零纹波的取得只是把互相耦合的两个线圈中的纹波都推向(或集中在)一个线圈中，余下的一个线圈流过的电流为直流电流。

2.2 从磁路理论说明纹波降低的原理^[2][3]

两电感的绕制情况如图2。

两个耦合电感的等效磁路模型与变压器的漏感模型(图3)是相同的，绕组1的耦合系数可定义为

k₁=（9）

式中：φ_m和φ_l1如图2所示。

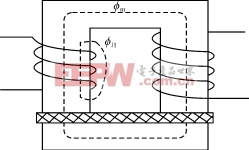
图2 电感UI绕线结构

因为v=Ndφ/dt，上式也可写成

k₁=（10）

根据等式Nφ=Li可得

k₁= (11)

因此k₁可看成是图3所示模型中电感电压的分压系数。图中理想变压器原边电压v_ip与输入电压有相同的形状，只是幅值减少了k₁倍。选择变压器变比N₁/N₂使变压器副边电压等于原边输入电压v，相同的电压同时加在电感L_l2两端，所以L_l2上的电流纹波将为零(di/dt=vL_l2/L_l2=0)。因此，电感L_l2上电流零纹波的条件为

k₁=N₁/N₂ (12)

图3 耦合电感的等效电路模型

这个条件可以这样理解，两绕组的匝比必须完全补偿初级绕组的漏磁通，从而使原边绕组在副边感应出的电压等于原边给定电压。

2.3 利用等效磁阻模型推导耦合电感的计算公式

图4为耦合电感的UI绕线结构图及其T型磁阻等效模型。因为，其中一个绕组中通有直流电流，为了防止磁芯饱和，图中磁芯需加气隙。且从后面的分析可知，绕在同一磁芯上的两个电感绕组就是通过调整气隙大小才能实现零纹波的。

图4（b）中，R_x1、R_x2分别为两气隙的磁阻，R₁为磁芯的磁阻。计算公式如下：

R_xi=x_i/μ₀S_e

R_l=l_e/μ₀S_e

式中：S_e和l_e分别为磁芯的等效截面积和等效磁路长度^[4]。