基于增量式PID控制的数控恒流源
3 系统的控制算法
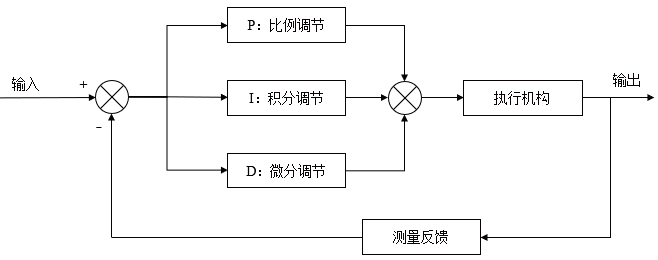
在恒流源的设计中,采用了增量式PID控制,由最为常见的传统式PID控制,比例、积分、微分控制推导而来。传统PID控制回路如图3所示。本文引用地址:https://www.eepw.com.cn/article/172154.htm

PID调节控制器的输出/输入关系的表达式如下:
![]()
式中:uT为输出信号,e(t)为输入偏差信号,tD为微分时间,tI为积分时间。在该系统中,单片机对恒流源模块输出进行采样,得出量化数值。所以需将式(1)离散化以求得所需结果:
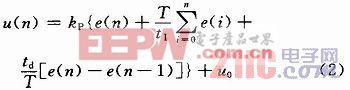
式中:T为采样周期;e(n)为第n次采样的偏差值;e(n-1)为第n-1次的采样偏差值;u(n)为第n次采样输出值。为使系统具有足够高的精度,必须将采样周期设定的足够小。由式(2)可以看出,如果要得出第n次输出值,需要处理的数据非常庞大,不仅需本次与前一次的偏差信号,而且需要从第一次到第n次的采样偏差值,再将其累加求和。在这一步骤当中,对微控制器所需的内存会有一定要求,并且其计算量繁冗。因此,对其进行化简,由递推原理求得第n-1次输出值,如下:

由式(4)可知,如果要得出第n次的输出值,只需求得第n-1次的采样输出值,第n,n-1,n-2次的偏差值,整个过程就简单清晰的多。在该系统中,经过A/D转换所得到的参数就是PID的被控对象。
在整个系统中,通过采用PID控制算法,不仅可以即时的反应出控制系统的偏差信号,减少偏差,而且通过积分控制作用之后,可以消除静差,使系统的精度大幅度提高。另外,在微分控制当中,偏差信号的变化趋势也可以读出。通过反馈作用,可对信号进行修正,从而加快系统的响应速度,减少调节时间。并且可避免因处理器的任何故障而引起的输出信号的大幅度变化。
为了证明增量式PID控制相对于传统PID控制的优越性,本文采用Matlab分别对增量式PID算法和传统PID算法进行仿真比较。
取KP=10,tD=3,tI=0.1,采样时间Ts=0.001。
pid控制器相关文章:pid控制器原理








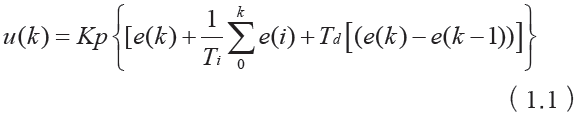
评论