欣赏波特图的魅力

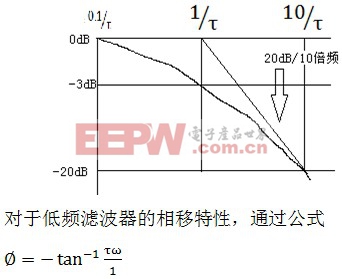
　　计算。

　　由于正切函数是非线性的，描述其特性比较难搞，其实我们可以依据我们拥有的基础数学知识来近似描述该函数：

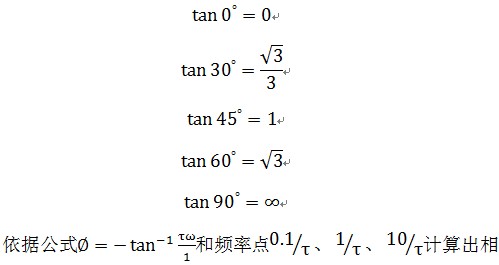
　　位为0°、45°和90°。在波特图的相频图中画出相应曲线，如下图所示：

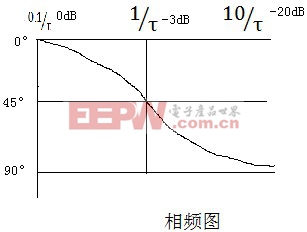
　　以上以一简单的一阶低通滤波器作为例子进行系统的波特图分析和画制，在实际的工程中，常常会因为采用多个电容和电阻构成了更加负责的系统，其实原理分析都是如此，只不过在分析过程中，找出关键位置的频率点，就能掌握系统传递函数的纲要，达到高屋建瓴的效果。

　　在多极点和零点传递函数中，使分母为零的频率点叫极点，使分子频率为零的频率点叫零点，极点可以使增益曲线下降，零点使增益曲线上升。在多极点和零点的系统中，只要找到各个极点和零点，找出其特性，将各个增益曲线叠加即可实现系统的极零分析，这个定理可以帮助大家在画多极点和零点的传递函数有个直观的印象。

　　对于一个电子工程师来说，不但能构建硬件电路，还需要有灵活的数学知识进行支持，才能将波特图理解更加透彻，这，就是学科交叉的魅力所在。

　　如果你对波特图感兴趣，欢迎到论坛单片机留贴，我们共同探讨。