多变量系统辨识及其PID解耦控制的研究
对于图1中的典型系统,当系统稳定后,断开u1、u2,给u2加入阶跃信号,记录下y1、y2的值,然后代入式(2)~式(12)辨识出G11(s),G21(s)。同理,u2加入阶跃信号,令u1=O,辨识出G12(s),G22(s),从而系统的传递函数矩阵求出

2 滞后环节近似
由于得出的模型含有滞后环节,而滞后环节不能够直接解耦,所以比较各种近似方法,通常近似方法为:一阶pade近似、二阶对称pade近似、二阶非对称Pade近似。文献对其多次进行实验发现一阶Pade逼近在初始时刻有波动,但在滞后较大的情况下逼近效果较好,这是因为Pade逼近引入零点的原因,二阶对称Pade逼近效果最差,而且二阶对称Pade逼近除了在初始时刻有波动还产生了超调量。二阶非对称Pade逼近调节时间较短,且无明显的超调量,但是波动较大。因此采用移位处理和二阶泰勒级数展开即全极点近似法

通过仿真验证发现全极点型近似方法由于避免引入零点,所以误差最小,其要比Pade逼近调节时间短,而且没有超调量,即能更好的获得阶跃响应特性。
3 解耦控制
多输入多输出系统内部结构复杂,存在有一定程度的耦合作用,对于这种存在耦合的对象,工业过程控制要求系统能够安全稳定地运行,又有较好的调节性能,能以较小的误差跟踪设定值的变化,并使稳态误差为零。为了达到高质量的控制性能,必须进行解耦设计。如何把它们间的耦合作用去掉变成独立的单变量系统进行控制是解决多变量控制的一种重要的方法,去掉耦合的过程就是解耦。其中常用的解耦方法有对角矩阵法、逆Nyquist曲线法和特征曲线法。其中对角矩阵法在过程控制领域中起到很大作用。

式(15)是一个多变量系统传递函数矩阵,对角矩阵解耦就是将耦合对象传递函数矩阵变成一个对角形矩阵的形式即式(16)所示,除主对角线上的元素外,其他元素均为零。这样输入U(s)与输出Y(s)就成为一一对应关系,以达到便于控制的目的。
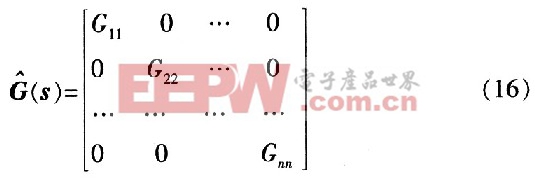
假设为了使传递函数矩阵转变为对角阵,在U(s)的输出端加入一个n×n的矩阵D(s)

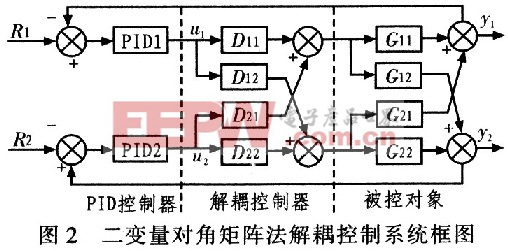
由于采用上文所提的方法辨识出的模型是奇异矩阵的几率很小,以二输入二输出系统为例,假设G(s)为一个非奇异方阵,则有逆矩阵存在。针对PID控制器的解耦控制系统框图如图2所示。本文引用地址:https://www.eepw.com.cn/article/162892.htm
pid控制器相关文章:pid控制器原理






评论