基于自适应模糊PID控制的太阳光跟踪伺服系统
3.2 确定语言变量和语言值的隶属度函数
设定输入误差e的语言变量为E,误差变化率的语言变量为EC,两者的论域都为{-3,-2,-1,0,1,2,3},相应的语言值为{负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB)};输出KP的语言变量为△KP,KI的语言变量为△KI,KD的语言变量为△KD,三者的论域都为{0,1,2,3},相应的语言值为{零(ZO),正小(PS),正中(PM),正大(PB)}。输入输出变量的隶属度函数采用三角函数。图2所示是输入变量e的隶属度函数,输出变量KP的隶属度函数如图3所示。本文引用地址:https://www.eepw.com.cn/article/159674.htm
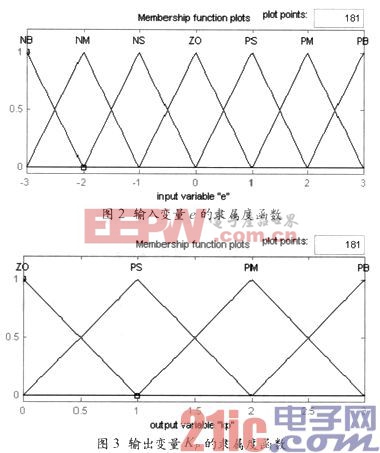
3.3 建立模糊控制规则
PID参数的适应必须考虑到在不同时刻三个参数的作用以及相互之间的互联关系。对于不同的误差e和误差变化率,控制器参数的自整定原则可归纳如下:
(1)当误差较大时,为使系统具有较好的快速跟踪性能,应取较大的KP和较小的KD参数;同时为避免系统响应出现较大的超调,应对积分作用加以限制,并取较小的KI。
(2)当误差处于中等大小时,为使系统响应具有较小的超调,KP应取小一些;同时为保证系统的响应速度,KI和KD的大小要适中。
(3)当误差较小时,为保证系统具有较好的稳态特性,KP和KI应取得大一些。同时为避免系统在设定值附近出现振荡,并考虑系统的抗干扰性能,当误差变化率较小时,KD可取大些;当误差变化率较大时,KD应取小一些。
按以上原理并根据PID参数自适应原则和操作经验所列出的输出变量模糊控制规则如表1所列。
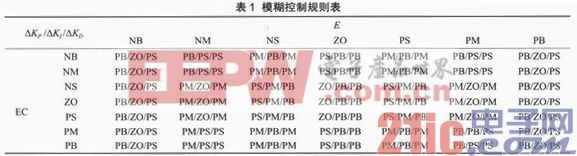
3.4 模糊量的清晰化
所谓模糊量的清晰化,就是把模糊推理后得到的模糊集转化为控制的数字值。这里采用重心法对模糊量进行清晰化。重心法是取隶属度函数曲线与横坐标围成面积的重心作为模糊推理的最终输出值,即:
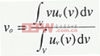











评论