针对语音信号的低功耗数字接收机解调方案

　　的实部和虚部均为正。所以，带通滤波器的系数有这样的特点：实部偶对称，虚部奇对称。

　　3 解调方案二

　　还是以解调上边带为例，先搬移待解调信号的频谱，再做低通滤波，最后又将信号的频谱搬移回来，如图7所示。这种方案滤波器的设计思路简单，但要对信号进行两次频谱搬移。

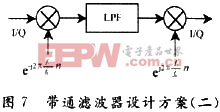
　　LPF与方案一中所设计的低通滤波器相同。如图8所示，信号被搬至零中频处。

　　4两种方案的比较

　　方案一中，带通滤波器在一个时钟周期内进行如下的计算：

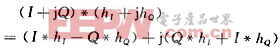
　　其中*表示卷积运算，下同。这表示要做4N次乘加运算，考虑到对称性只需要2N次乘加运算。

　　如果信号不是独立边带的，上边带信号解调所用的带通滤波器的系数与下边带信号解调所用的带通滤波器的系数是共轭关系，即hUSB(n)=hLSB*(n)，则另外一个边带的滤波计算为：

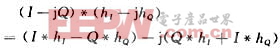
　　其结果与前面的成共轭关系，因此，只要得到其中一个边带的实数部分即可得到解调结果。这样只需要N次乘加运算。

　　如果是独立边带的，上下边带的共轭关系不存在，则解调其中一个边带需要2N次乘加运算，上下边带解调共需要4N次乘加运算。

　　方案二中，低通滤波器在一个时钟周期内进行如下的计算：

　　这表示要做2N次乘加运算，考虑到对称性只需要N次乘加运算。

　　如果信号不是独立边带的，那么同方案一，只需要N/2次乘加运算。如果信号是独立边带的那就上下边带解调共需要2N次乘加运算。

　　另外两次经过NCO的运算在一个时钟周期内共需要8次乘加运算。

　　综合来说，就运算开销方面而言方案二要优于方案一。